|
|
源自知乎提问
题:在三角形 $ABC$ 中 $2BC^2+AB^2=2AC^2$ 且点 $D$ 在 $BC$ 延长线上满足 $DA=DB$,则 $\angle DAC$ 的最大值为________.
以下从边着手,算一算. 节省时间版:直接看倒数六行即可.
易知 $\color{blue}{2\overrightarrow {AB}\cdot\overrightarrow {AD}}=AB^2+AD^2-BD^2.$
设 $\overrightarrow {BC}=\lambda \overrightarrow {BD},$ 即 $\overrightarrow {AC}-\overrightarrow {AB}=\lambda (\overrightarrow {AD}-\overrightarrow {AB})$
整理即为 $\overrightarrow {AC}=\lambda \overrightarrow {AD}+(1-\lambda) \overrightarrow {AB},$
两边平方有
\begin{align*} \color{#FF0022}{AC^2}&=\lambda^2 AD^2+(1-\lambda)^2 AB^2+\lambda(1-\lambda)\cdot \color{blue}{2\overrightarrow {AB}\cdot\overrightarrow {AD}}\\[1em] &=\lambda^2 AD^2+(1-\lambda)^2 AB^2\\[1ex]&\quad+\lambda(1-\lambda)(AB^2+AD^2-BD^2)\\[1em] &\color{#FF0022}{=\lambda AD^2+(1-\lambda) AB^2-\lambda(1-\lambda)BD^2}\qquad{(*)}, \end{align*}
(这就是三角形中著名的 Stewart 定理,与 Ptolemy 定理等价.)
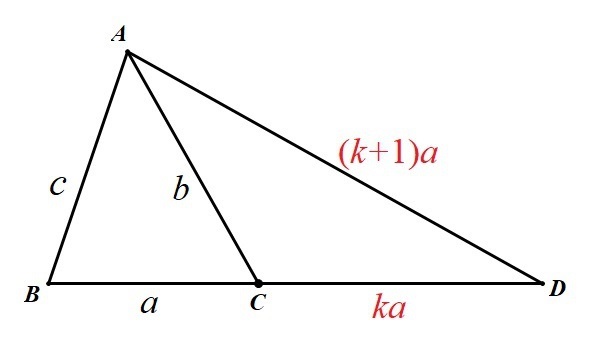
图 1 可求得 k 为 1
记三角形 $ABC$ 的三个顶点 $A,B,C$ 所对的三边分别为 $a,b,c$.
并设 $CD=ka$ 则 $\lambda=\frac {BC}{BD}=\frac a{a+ka}=\frac 1{k+1},$ $AD=BD=(k+1)a$ .
于是 $(*)$ 式即为
$\color{#FF0022}{b^2=\frac 1{k+1} (k+1)^2a^2+\frac k{k+1} c^2-\frac k{(k+1)^2}(k+1)^2a^2}, $ 亦即
$$b^2=a^2+\frac k{k+1}c^2.$$
与条件 $b^2=a^2+\frac 12c^2$ 对照知 $\frac k{k+1}=\frac 12$ 即 $k=1.$
从而在三角形 $ACD$ 中,如图 1,
$$\cos DAC=\frac {b^2+4a^2-a^2}{2b\cdot 2a}=\frac {b^2+3a^2}{4ab}\geqslant \frac {2\sqrt 3ab}{4ab}=\frac {\sqrt 3}2,$$
所以 $\angle DAC\leqslant \frac {\pi}6.$ |
|