几何最值问题

facebooker

已知：$x^2+y^2=4$,求$3\sqrt{5-2x}+\sqrt{13-6y}$的最小值
是不是阿氏圆啊？咋做呢？

kuing

嗯，配个方，很明显，原式 `=3\sqrt{(x-1)^2+y^2}+\sqrt{x^2+(y-3)^2}`。

敬畏数学

forum.php?mod=viewthread&tid=5129

kuing

回复 3# 敬畏数学

是的，同样的题，反正就是配方+阿氏，就数据上来说，目测 1# 的还简单一些。

facebooker

大佬 没学过阿氏圆啊 给个过程吧 谢谢

kuing

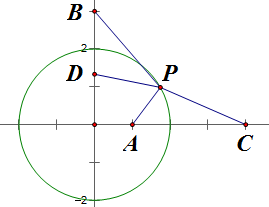
设 `P(x,y)` 在圆 `x^2+y^2=4` 上，记 `A(1,0)`, `B(0,3)`，据 2# 的配方式可知问题即是求 `3PA+PB` 的最小值。

设 `C(4,0)`, `D(0,4/3)`，则不难证明
\[PA=\frac12PC,PB=\frac32PD,\]从而
\[3PA+PB=\frac32(PC+PD)\geqslant\frac32CD=\frac32\sqrt{4^2+\frac{4^2}{3^2}}=2\sqrt{10},\]取等为线段 `CD` 与圆的交点，显然存在，不必具体写出。