Last edited by hbghlyj 2020-7-9 00:41轮换连接凸四边形的各边和下一条边中点的直线围成一个四边形,证明
(1)四边形是凸的
(2)其面积与原四边形的面积之比的范围是(1/6,1/5]
由于仿射变换保持中点、凸性和面积比,不妨设原四边形的四顶点为$A_1(0,1),A_2(0,0),A_3(1,0),A_4(a,b)$,原四边形是凸的等价于$a>0,b>0,a+b>1.$
(2)四直线围成的四边形面积与原四边形的面积之比$k=\frac AB$,其中$A=a^4+(22b+12)a^3+(41b^2+27b-19)+(28b^3+9b^2-11b+8)a+4b^4+6b^3-b^2-4b-1,B=(3a+b+1)(2a+4b-1)(4a+3b-2)(a+2b+2)$
为证明$ k\le\frac15$,我们有$B-5A=(a+2b-3)^2(2a-b-1)^2\ge0,\therefore$
当且仅当$b=\frac{3-a}2,0<a<3$或$b=2a-1,a>\frac23$时取等,即下图的蓝色线段和蓝色射线
$b=\frac{3-a}2\Leftrightarrow\frac{\frac b2-1}{\frac{a+1}2}=-\frac12,b=2a-1\Leftrightarrow\frac{b+1}a=\frac b{a-\frac12}$
而仿射保持平行,因此对于一般的四边形,当且仅当围成的四边形至少有一组对边平行时k取得最大值$\frac15$
为证明$k>\frac16$,我们有$6A-B=5(ab+2b^2+4a-2)(2a^2+4ab-3a+b+1)$.
$ab+2b^2+4a-2=b(a+b)+b^2+4a-2>b^2+4a+b-2>b^2+3a-1>4-3b+b^2\ge0$
取等时b=1,a=0
$2a^2+4ab-3a+b+1=(a-1)^2+b+3ab+a(a+b-1)>(a-1)^2+b+3ab>0$
取等时a=1,b=0
因此,当且仅当b=1,a=0或a=1,b=0时k取得最小值,此时原四边形和围成的四边形都退化为三角形
动画演示:
Maple代码:- area := proc(ngon)
- local i,s,nvs;
- nvs := nops(ngon);
- s := 0;
- for i from 2 to nvs-1 do
- s := s+ linalg[det]( array(1..2,1..2,[
- [op(expand(ngon[ (i-1) mod nvs +1]- ngon[1])) ],
- [op(expand(ngon[i mod nvs +1]-ngon[1])) ] ])) od;
- 1/2*s end:
- ngon := [[0,0],[1,0],[a,b],[c,d]];
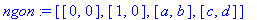
nvs := nops(ngon);
- mids := [seq(1/2*(ngon[(i-1) mod nvs + 1] +ngon[i mod nvs + 1]),i=1..nops(ngon))]:
- segs := [seq([(mids[(i-1) mod nvs + 1] ,ngon[(i+1) mod nvs + 1])],i=1..nops(ngon))]:
- insect := proc(seg1,seg2)
- local sol,t,r,eqns;
- eqns := expand(t*seg1[1]+(1-t)*seg1[2]- r*seg2[1]-(1-r)*seg2[2]);
- sol := solve({eqns[1],eqns[2]},{t,r}):
- subs(sol,expand(t*seg1[1]+(1-t)*seg1[2])) end:
- getnewgon := proc(ngon)
- local i,nvs,mids,segs;
- nvs := nops(ngon);
- mids := [seq(1/2*(ngon[(i-1) mod nvs + 1] +ngon[i mod nvs + 1]),i=1..nops(ngon))];
- segs := [seq([(mids[(i-1) mod nvs + 1] ,ngon[(i+1) mod nvs + 1])],i=1..nops(ngon))]:
- map(simplify, [seq(insect([mids[(i-1) mod nvs +1],ngon[(i+1) mod nvs +1]], [ngon[i mod nvs +1],mids[(i+2) mod nvs +1]]),i=1..nvs)]);
- end:
- newgon:= getnewgon(ngon);
- f := unapply(simplify(area(newgon)/area(ngon)),a,b,c,d);
- plgon:=(a1,b1,c1,d1) ->
- plots[display]([
- plots[polygonplot](subs({a=a1,b=b1,c=c1,d=d1},newgon),
- color=turquoise),
- plots[polygonplot](subs({a=a1,b=b1,c=c1,d=d1}, ngon),color=yellow),
- plot(subs({a=a1,b=b1,c=c1,d=d1},segs),color=red,thickness=3),
- plots[textplot]([.5,-.5,cat(`ratio =`,convert(evalf(f(a1,b1,c1,d1),5),string))])],scaling=constrained):
- plgon(2,3,0,1);
- factor(numer(f(a,b, 0,1)));
- top := collect(numer(f(a,b, 0,1)),a);
- bottom:=factor(collect(expand(denom(f(a,b,0,1))),a));
- lefthand := factor(bottom-5*top) ;
- pl1 := plot( 3/2-x/2,x=0..3 ,color=blue,thickness=2):
- pl2 := plot( 2*x-1,x=2/3..3 ,color=blue,thickness=2):
- righthand:= factor(6*top-bottom) ;
- pl1 := plot( 3/2-x/2,x=0..3 ,color=blue,thickness=2):
- pl2 := plot( 2*x-1,x=2/3..3 ,color=blue,thickness=2):
- frame := (x,y) -> plots[display]([plgon(x,y,0,1) ,pl1,pl2],view=[0..3,-.5..3],scaling=constrained):
- path := proc(lst,t0,t1,kind,m)
- local x,y,p,n;
- #lst := [[0,0],[1,0],[1,1],[2,3]];
- #kind := linear;
- #t0:=0:
- #t1:=1:
- n:=nops(lst)-1:
- #m:=10:
- readlib(spline);
- x :=unapply(spline( [seq(t0+j*(t1-t0)/n,j=0..n)],
- [seq(lst[i][1],i=1..n+1)],t,kind),t):
- y :=unapply(spline( [seq(t0+j*(t1-t0)/n,j=0..n)],
- [seq(lst[i][2],i=1..n+1)],t,kind),t):
- p := [x,y]:
- plots[display](
- [seq(frame(op(p(t0 +i/(m-1)*(t1-t0)))),i=0..m-1)],
- scaling=constrained,insequence=true); end:
- path([[2/3,1/3],[2/3,1/3],[1,1],[1,1],[3,0],[1,0],[1,0],[2,3],[2,3],[1,1],[1,1],[0,3/2],[0,1],[0,1],[2,3],[2/3,1/3]],0,1,linear,75);
- frame(2,3/2-1/2*2);
|