一道与阿氏圆相关的几何题，希望用初中解法

lrh2006

请教一个问题，请用初中生能看懂的方法做，不要用导数这些，最好能用到阿氏圆。谢谢大家！
已知△ABC的面积为定值，∠A的平分线交BC于点D,AB=2AC,且AD=kAC,当BC的长度最短时，k=？
答案提示：当点A到BC距离最大时，BC长度最小，此时点A到BC距离为阿氏圆的半径。答案是5分之2根号10

kuing

阿氏圆对于初中生也未必会熟悉，初中解法可以这样：

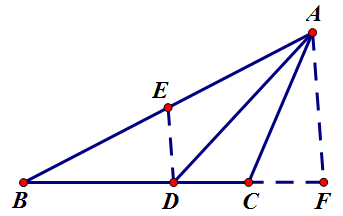
如图，取 `AB` 中点 `E`，则 `\triangle AED\cong\triangle ACD`，
延长 `BC` 至 `F` 使 `CD=CF`，则由 `AB=2AC` 得 `DB=2DC=DF`，故 `DE` 为 `\triangle ABF` 的中位线，所以 `\angle FAD=\angle EDA=\angle FDA`，即 `\triangle FAD` 为等腰三角形。

要 `BC` 最短相当于要 `\triangle FAD` 的腰最短，而由 `\triangle ABC` 面积为定值知 `\triangle FAD` 的面积也为定值，所以当且仅当 `FA\perp FD` 时腰最短，此时不妨设 `FA=FD=2`，则 `AD=2\sqrt2`, `AC=\sqrt5`，故 `k=AD/AC=2\sqrt{10}/5`。

PS、标题一如既往地短……
PS2、你啥时候上上Q呀……

其妙

下面链接例文章的中后半部分有阿氏圆：blog.sina.com.cn/s/blog_54df069f0101j39b.html，
角平分线的比例是1:2，在链接里是1:3，是类似的，
不过用的建立坐标系做的，也可以从特殊点找到阿氏圆的直径，就好办了

lrh2006

知道了，谢谢楼上两位哟。论坛真好
PS、不知道怎么写标题才合版主的心意...你就帮我改改嘛，或者，教教我？
PS2、我有上的啊。只是前阵子手机手提都坏了，拿去修，把我QQ都弄不好了...

kuing

回复 4# lrh2006

已改，其实就是放点关键词上去就好了，答案提到阿氏圆，这就是个很好的关键词，至于后半句可加可不加……

hbghlyj

其妙 发表于 2019-8-3 21:35
下面链接例文章的中后半部分有阿氏圆：http://blog.sina.com.cn/s/blog_54df069f0101j39b.html，
角平分线 ...

系统维护中，博文仅作者可见。登陆后可查看本人文章。