|
|
 kuing
kuing
posted 2020-3-4 14:04
刚刚群里一题差不多也放这里存一下:
鄂B****林(3086*****)
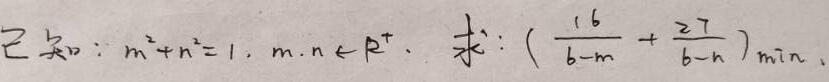
阅A****k(249533164)
\[\frac{16}{6-m}+\frac{27}{6-n}=\frac{77}{10}+\frac{192(m+n-1)+11n(10-7m)}{10(6-m)(6-n)}>\frac{77}{10},\]`n\to0`, `m\to1` get "="
鄂B****林
这个不是一般难难配啊
阅A****k
这是装逼解法,没啥意义的
鄂B****林
我以为柯西降次,能配凑,可总搞不出来
粤A****巡
主要是求最小值...
在边界取到
弄那些乱七八糟的不等式顶多弄出最大值
阅A****k
最大值是高次方程,最小值在边界反而有得玩
下面将题目改成:已知 `m`, `n\in[0,6)` 且 `m+n\geqslant1`,求 `16/(6-m)+27/(6-n)` 的最小值。
解:
(1)若 `m>1`,则
\[\frac{16}{6-m}+\frac{27}{6-n}>\frac{16}5+\frac{27}6=\frac{77}{10};\]
(2)若 `m\leqslant1`,由条件得 `6-n\leqslant5+m`,故
\[\frac{16}{6-m}+\frac{27}{6-n}\geqslant\frac{16}{6-m}+\frac{27}{5+m}=\frac{77}{10}+\frac{11(1-m)(10-7m)}{10(6-m)(5+m)}\geqslant\frac{77}{10};\]
综上所述,原式 `\geqslant77/10`,当 `m=1`, `n=0` 取等。 |
|