|
|
**寒，**珊 10:42:36
高线的垂足形成的三角形，其外接圆半径与原三角形外接圆半径有什么关系吗？
kuing 15:27:17
两倍关系
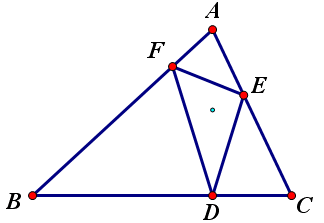
\[2R_{\triangle ABC}=\frac{BC}{\sin A}, 2R_{\triangle DEF}=\frac{EF}{\sin\angle EDF},\]故
\[\frac{R_{\triangle ABC}}{R_{\triangle DEF}}=\frac{BC}{EF}\cdot\frac{\sin\angle EDF}{\sin A}=\frac{AB}{AE}\cdot\frac{\sin(\pi-2A)}{\sin A}=\frac{\sin 2A}{\cos A\sin A}=2.\]
kuing 15:46:22
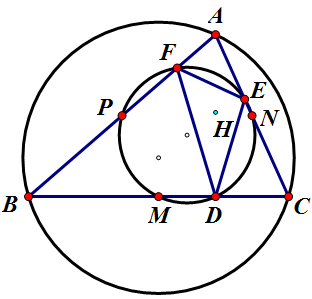
我发现好像小圆圆心在大圆圆心和垂心的中点上
kuing 16:01:33
哦，想起了九点圆，三垂足和三中点共圆，所以显然就是两倍关系了[笑哭]
|
|
乌贼
发表于 2020-3-8 18:22
