|
|
original poster
hbghlyj
posted 2020-3-20 00:26
Last edited by hbghlyj 2020-3-20 13:41(1)我觉得应该是存在的。取一个特例研究一下。如果在这种情况下是存在的,那么就能说明它的存在性,然后就成了
$\alpha\in(0,\pi),A(0,0,0),B(1,0,0),C\left(1+\frac{\cos\alpha}{\sqrt2},\sin\alpha,\frac{\cos\alpha}{\sqrt2}\right),D\left(\frac{\cos\alpha}{\sqrt2},\sin\alpha,\frac{\cos\alpha}{\sqrt2}\right),A_1(0,0,1),B_1(1,0,1),C_1\left(1+\frac{\cos\alpha}{\sqrt2},\sin\alpha,1+\frac{\cos\alpha}{\sqrt2}\right),D_1\left(\frac{\cos\alpha}{\sqrt2},\sin\alpha,1+\frac{\cos\alpha}{\sqrt2}\right)$,那么$ACB_1D_1$是正交四面体,则内切球半径$r=\frac{2\sin α}{\sqrt{3+\sqrt2\cos\alpha}+\sqrt{3-\sqrt2\cos\alpha}+2\sqrt{2-\cos2\alpha}}$
内心I(a,b,a),其中
$a=\frac{r (\sqrt{3 + 2\sqrt2 \cos α} + (1+ \sqrt2 \cos α )\sqrt{1+2\sin^2\alpha})}{2\sin\alpha}$
$b=r \sqrt{1 + 2\sin^2α}$
垂心H$\left(\frac{-\sqrt{2} \sin ^2\alpha +3 \cos \alpha +2 \sqrt{2}}{2 \cos \alpha +2 \sqrt{2}},\frac{\left(\sqrt{2} \cos \alpha +1\right) \left(\sqrt{2} \sin \alpha -\cot \alpha \right)}{2 \cos \alpha +2 \sqrt{2}},\frac{-\sqrt{2} \sin ^2\alpha +3 \cos \alpha +2 \sqrt{2}}{2 \cos \alpha +2 \sqrt{2}}\right)$
重心G$\left(\frac12+\frac{\cos\alpha}{2\sqrt2},\frac{\sin\alpha}2,\frac12+\frac{\cos\alpha}{2\sqrt2}\right)$
$IG^2$和$r^2$的图像有两个交点,所以有两个解
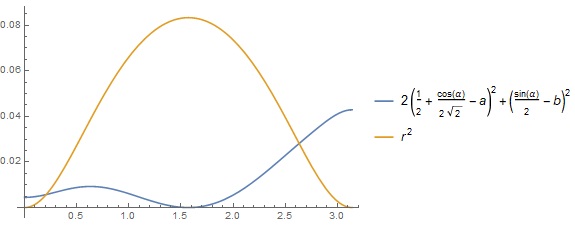
近似值为0.20716368090533166与2.632344071200761
$IH^2$和$r^2$的图像有两个交点,所以有两个解
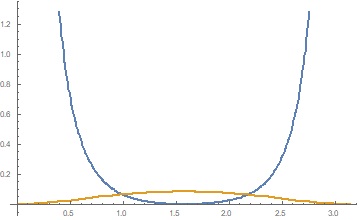
近似值为0.9872604197192401,2.1763406692333445 |
|