代数数化为方程的根RootReduce

kuing

In[1]:= RootReduce[Sqrt[2] + Sqrt[3]]
Out[1]= Root[1 - 10 #1^2 + #1^4 &, 4]

反过来可以用 ToRadicals

abababa

回复 1# kuing
这里的#1就相当于x的意思吧，后面那个&，还有4表示的是什么呢？

kuing

回复 2# abababa

4好像表示第4个根……至于根按什么规则来排列我也不清楚……有空查查帮助看看有没有

abababa

回复 3# kuing
谢谢，试了几个确实都表示根的次序。

青青子衿

回复 1# kuing

In[1]:= RootReduce[Sqrt[2] + Sqrt[3]]
Out[1]= Root[1 - 10 #1^2 + #1^4 &, 4]
反过来可以用 ToRadicals ...
kuing 发表于 2013-7-27 20:09

In[1]:=MinimalPolynomial[Sqrt[2] + Sqrt[3], x]
Out[1]:=1 - 10 x^2 + x^4

isee

回复 5# 青青子衿


    太强大了！如何按降幂排列？即 MinimalPolynomial[Sqrt[2] + 1, x] // TraditionalForm

hbghlyj

青青子衿 发表于 2014-6-26 13:19
In[1]:=MinimalPolynomial[Sqrt[2] + Sqrt[3], x]
Out[1]:=1 - 10 x^2 + x^4

见西西的10道题第9道:
若 $p$ 和 $q$ 是不同的素数, 证: $[\mathbb Q(\sqrt{p}, \sqrt{q}):\mathbb Q]=4$, 并且 $\mathbb Q(\sqrt{p}, \sqrt{q})=\mathbb Q(\sqrt{p}+\sqrt{q})$

hbghlyj

kuing 发表于 2014-6-21 05:24
4好像表示第4个根……至于根按什么规则来排列我也不清楚……
查查帮助看看

$\tt Root[f,k]$ represents the exact k^th root of the polynomial equation $\tt f[x]==0$.

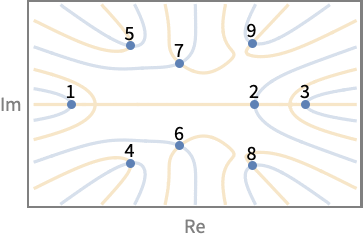
The root indexing representation $\tt Root[f,k]$ applies to polynomial functions $\tt f$ only. The indexing of roots takes the real roots first, in increasing order. For polynomials with rational coefficients, the complex conjugate pairs of roots have consecutive indices.