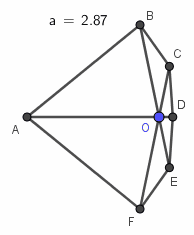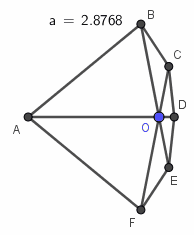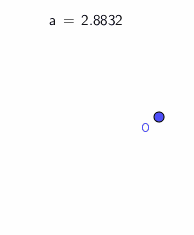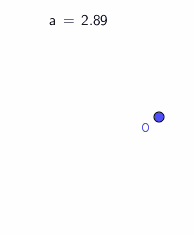
|
|
凸六边形ABCDEF,AB=AF=AD=BE=CF=a,BC=EF=CD=DE=1,求a的最大值.
分析一下条件的个数,可以发现,这个六边形如果存在,就只能有有限个.
设AO=x,BO=y,则DO=d-x,CO=e-y,设∠AOB=∠COD=α($0<\alpha<\frac\pi2$),
由余弦定理,$\led-2 x y\cos \alpha+x^2+y^2=a^2\\-2 (a-x) (a-y)\cos \alpha+(a-x)^2+(a-y)^2=a^2\\2 \left(2 \cos^2 \alpha-1\right) y (a-y)+(a-y)^2+y^2=1\endled$,
消去x,y得$8 a^4 \cos ^3\alpha -12 a^4 \cos ^2\alpha +4 a^4 \cos \alpha -4 a^2 \cos \alpha -a^4+6 a^2 -1=0$
计算$\cos\alpha$的判别式:$-64 (a-1)^2 a^8 (a+1)^2 \left(23 a^4-194 a^2+27\right)\ge0$说明a必须介于方程$23 a^4-194 a^2+27=0$的两正根(约为0.376232和2.8798)之间才能有实数解.即
$\sqrt{\frac{97-26 \sqrt{13}}{23}}\le a\le\sqrt{\frac{26 \sqrt{13}+97}{23}}$
用ggb画出图就会看到一个不连续的现象：当a慢慢接近2.8798时图形几乎没有变化,当a=2.8798时也没变化(这时方程有两个相等的实根),当a>2.8798时图形突然消失了(那两个实根变成了虚根).整个过程中六边形都是凸的.
注:如果放到直觉去想一下,这是不太可能的,因为六边形的边长连续改变,如果一直是凸的,怎么可能弄不动而卡死呢.哈哈,还是代数描述精确一些.
|
|
kuing
发表于 2020-10-15 22:39
