Last edited by hbghlyj 2021-3-1 10:12圆$O_1,O_2$,半径为$r_1,r_2$.直线与圆$O_1$交于C,D,与圆$O_2$交于E,F,$\overparen{CD}\pm\overparen{EF}=\pi$,直线与一条关于$O_1O_2$对称的双曲线相切.
证明:首先,我们有引理:直线到两点$O_1,O_2$的距离为$d_1,d_2$,$Ad_1^2+Bd_2^2$为定值(A,B为常数),则直线与一条二次曲线相切.
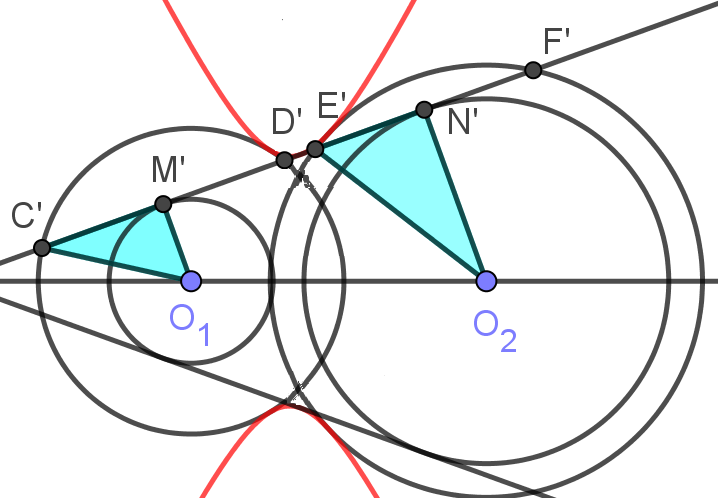
回到原题,设CD,EF的中点为M,N,则$\triangle CO_1M\sim\triangle O_2EN$.由$CO_1^2=CM^2+O_1M^2$和引理,命题得证.
推论1:$\alpha$是任意实数,以$O_1$为圆心,$r_1\cos α$为半径作圆c.以$O_2$为圆心,$r_2\sin α$为半径作圆d,四条直线均与曲线相切.
推论2:双曲线与圆$O_1,O_2$均相切.
证明:当圆$O_1$与圆c重合时,圆d缩成一点,四条公切线退化为d到圆$O_1$的两条切线dX,dY,它们也是双曲线的切线.
两条公切线CD,C'D'与双曲线的两个切点和CD,C'D'的交点重合,而CD,C'D'的交点的极限是X,所以X在双曲线上.因此双曲线与圆$O_1$相切于X,Y.

|