关于内切圆的六道题和一道欧拉线有关的题

hbghlyj

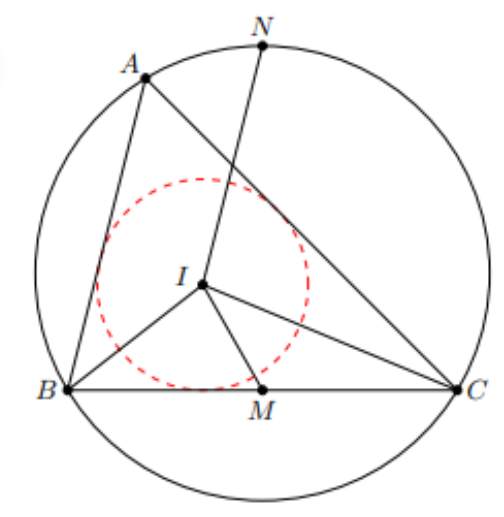
1.I是△ABC的内心,M是BC中点,N是弧BAC中点,求证∠BIM+∠CIN=180°

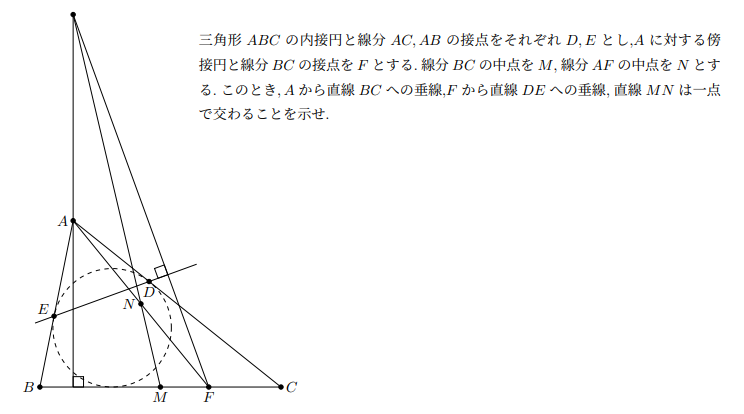
2.M是BC的中点,D,E是内切圆切点,F是A-旁切圆与BC的切点,N是AF中点,求证:过A的高线,MN,过F的DE垂线三线共点.

3.AB≠AC,I是△ABC的内心,D是内切圆与BC的切点,M是BC中点,MI交AC于E,E在BC上的投影为F,求证AE=DF.

4.AB≠AC,I是△ABC的内心,D,E,F是内切圆切点,△DEF的旁心为$I_D,I_E,I_F$,求证$ A I_{D}, B I_{E}, C I_{F} $形成的三角形的垂心为I.

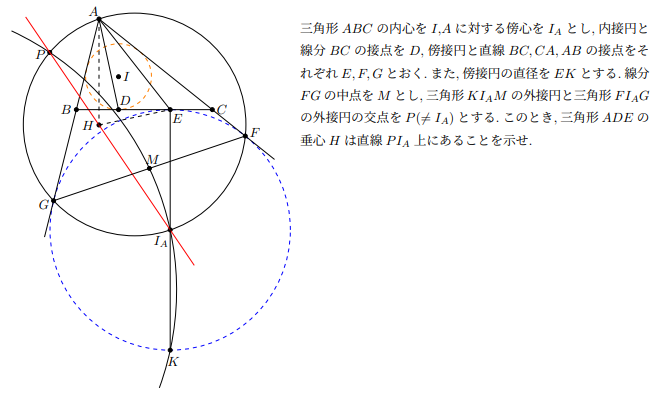
5.I是△ABC的内心,$I_A$为A-旁心,内切圆与BC切于D,A-旁切圆的切点为E,F,G,EK为A-旁切圆的直径.M为线段FG的中点,设P(≠$I_A$)为圆$I_A$KM与圆AFG的交点,证明△ADE的垂心H在P$I_A$上.

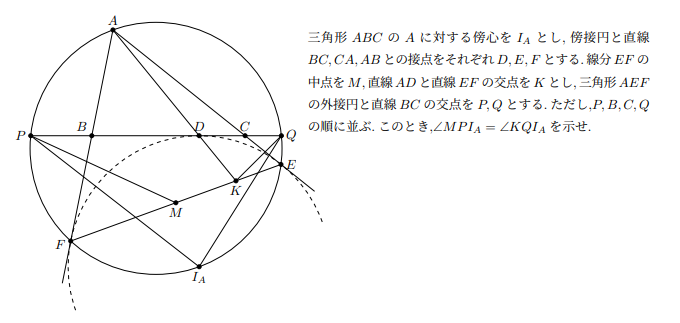
6.设$I_A$是△ABC的A-旁心.D,E,F是A-旁切圆切点.M是EF中点.AD交EF于K.设P和Q是圆AEF与BC的交点,排列顺序是P,B,C,Q.求证$ \angle M P I_{A}=\angle K Q I_{A} $

7.对于非等边三角形ABC,BD和CE是高,M和N是AB和AC的中点.DM交EN于P.证明P在△ABC的欧拉线上(红色线).

hbghlyj

7可以用面积法消点
设P′为DM和GH的交点.只需证\(\frac{DP}{MP} = \frac{DP′}{MP′}\).
因为\(\frac{DP′}{MP′} = \frac{\left( - S_{GHD} \right)}{\left( - S_{GHM} \right)}\)
只需证1\(= \frac{\frac{DP}{MP}\left( - S_{GHM} \right)}{\left( - S_{GHD} \right)}\)
因为\(\frac{DP}{MP} = \frac{\left( - S_{NED} \right)}{\left( - S_{MNE} \right)}\)
只需证1\(= \frac{\left( - S_{NED} \right)\left( - S_{GHM} \right)}{\left( - S_{GHD} \right)\left( - S_{MNE} \right)}\)
因为\(S_{GHD} = \frac{1}{3}\left( S_{HDC} + S_{HDA} \right)\)
\(S_{GHM} = \frac{1}{3}\left( S_{HMC} + S_{HMB} + S_{HMA} \right)\)
只需证1\(= \frac{\left( - S_{NED} \right)\left( - S_{HMC} - S_{HMB} - S_{HMA} \right)3}{\left( - S_{HDC} - S_{HDA} \right)\left( - S_{MNE} \right)3}\)
约去\(3\)
只需证1\(= \frac{S_{NED}\left( S_{HMC} + S_{HMB} + S_{HMA} \right)}{\left( S_{HDC} + S_{HDA} \right)S_{MNE}}\)
因为\(S_{HDA} = \frac{\left( - S_{DBA}S_{EDC} \right)}{S_{EDCB}}\)
\(S_{HDC} = \frac{S_{DCB}S_{EDC}}{S_{EDCB}}\)
\(S_{HMA} = \frac{\left( - S_{EDB}S_{MCA} \right)}{S_{EDCB}}\)
\(S_{HMB} = \frac{S_{ECB}S_{MDB}}{\left( - S_{EDCB} \right)}\)
\(S_{HMC} = \frac{\left( - S_{DCB}S_{MEC} \right)}{S_{EDCB}}\)
只需证1\(= \frac{S_{NED}\left( - S_{DCB}S_{MEC} - S_{ECB}S_{MDB} - S_{EDB}S_{MCA} \right)S_{EDCB}}{\left( \left( S_{DCB} - S_{DBA} \right)S_{EDC} \right)S_{MNE}S_{EDCB}}\)
约去\(S_{EDCB}\)
只需证1\(= \frac{- S_{NED}\left( S_{DCB}S_{MEC} + S_{ECB}S_{MDB} + S_{EDB}S_{MCA} \right)}{S_{EDC}\left( S_{DCB} - S_{DBA} \right)S_{MNE}}\)
因为\(S_{MNE} = \frac{1}{2}\left( \left( 2\frac{AE}{AB} - 1 \right)S_{NBA} \right)\)
\(S_{MCA} = \frac{1}{2}\left( - S_{CBA} \right)\)
\(S_{MDB} = \frac{1}{2}S_{DBA}\)
\(S_{MEC} = \frac{1}{2}\left( - 2S_{CBA}\frac{AE}{AB} + S_{CBA} \right)\)
只需证1\(= \frac{- S_{NED}\left( - S_{CBA}S_{EDB} + S_{DBA}S_{ECB} - 2S_{CBA}S_{DCB}\frac{AE}{AB} + S_{CBA}S_{DCB} \right)2}{S_{EDC}\left( S_{DCB} - S_{DBA} \right)\left( \left( 2\frac{AE}{AB} - 1 \right)S_{NBA} \right)2}\)
约去\(2\)
只需证1\(= \frac{S_{NED}\left( S_{CBA}S_{EDB} - S_{DBA}S_{ECB} + 2S_{CBA}S_{DCB}\frac{AE}{AB} - S_{CBA}S_{DCB} \right)}{S_{EDC}\left( S_{DCB} - S_{DBA} \right)S_{NBA}\left( 2\frac{AE}{AB} - 1 \right)}\)
因为\(S_{NBA} = \frac{1}{2}S_{CBA}\)
\(S_{NED} = \frac{1}{2}\left( \left( 2\frac{AD}{AC} - 1 \right)S_{ECA} \right)\)
只需证1\(= \frac{\left( \left( 2\frac{AD}{AC} - 1 \right)S_{ECA} \right)\left( S_{CBA}S_{EDB} - S_{DBA}S_{ECB} + 2S_{CBA}S_{DCB}\frac{AE}{AB} - S_{CBA}S_{DCB} \right)2}{S_{EDC}\left( S_{DCB} - S_{DBA} \right)S_{CBA}\left( 2\frac{AE}{AB} - 1 \right)2}\)
约去\(2\)
只需证1\(= \frac{S_{ECA}\left( 2\frac{AD}{AC} - 1 \right)\left( S_{CBA}S_{EDB} - S_{DBA}S_{ECB} + 2S_{CBA}S_{DCB}\frac{AE}{AB} - S_{CBA}S_{DCB} \right)}{S_{EDC}\left( S_{DCB} - S_{DBA} \right)S_{CBA}\left( 2\frac{AE}{AB} - 1 \right)}\)
因为\(S_{EDC} = \frac{\left( - P_{CAB}S_{DCB} \right)}{\left( - P_{ABA} \right)}\)
\(\frac{AE}{AB} = \frac{\left( - P_{CAB} \right)}{\left( - P_{ABA} \right)}\)
\(S_{ECB} = \frac{\left( - S_{CBA}P_{CBA} \right)}{\left( - P_{ABA} \right)}\)
\(S_{EDB} = \frac{\left( - P_{CBA}S_{DBA} \right)}{\left( - P_{ABA} \right)}\)
\(S_{ECA} = \frac{S_{CBA}P_{CAB}}{\left( - P_{ABA} \right)}\)
只需证1\(= \frac{S_{CBA}P_{CAB}\left( 2\frac{AD}{AC} - 1 \right)\left( \left( - 2S_{CBA}P_{CAB} + P_{ABA}S_{CBA} \right)S_{DCB} \right)\left( - P_{ABA} \right)\left( - P_{ABA} \right)}{\left( - P_{CAB}S_{DCB} \right)\left( S_{DCB} - S_{DBA} \right)S_{CBA}\left( - 2P_{CAB} + P_{ABA} \right)\left( - P_{ABA} \right)\left( - P_{ABA} \right)}\)
约去\(S_{DCB}P_{CAB}S_{CBA}\left( 2P_{CAB} - P_{ABA} \right)\left( P_{ABA} \right)^{2}\)
只需证1\(= \frac{- S_{CBA}\left( 2\frac{AD}{AC} - 1 \right)}{\left( S_{DCB} - S_{DBA} \right)}\)
因为\(S_{DBA} = \frac{\left( - S_{CBA}P_{CAB} \right)}{\left( - P_{ACA} \right)}\)
\(S_{DCB} = \frac{\left( - S_{CBA}P_{BCA} \right)}{\left( - P_{ACA} \right)}\)
\(\frac{AD}{AC} = \frac{\left( - P_{CAB} \right)}{\left( - P_{ACA} \right)}\)
只需证1\(= \frac{- S_{CBA}\left( - 2P_{CAB} + P_{ACA} \right)\left( - P_{ACA} \right)}{\left( S_{CBA}P_{CAB} - S_{CBA}P_{BCA} \right)\left( - P_{ACA} \right)}\)
约去\(S_{CBA}P_{ACA}\)
只需证1\(= \frac{- \left( 2P_{CAB} - P_{ACA} \right)}{- \left( P_{CAB} - P_{BCA} \right)}\)
因为\(P_{BCA} = \frac{1}{2}\left( P_{BCB} + P_{ACA} - P_{ABA} \right)\)
\(P_{CAB} = \frac{1}{2}\left( - P_{BCB} + P_{ACA} + P_{ABA} \right)\)
只需证1\(= \frac{- \left( - P_{BCB} + P_{ABA} \right)2}{- \left( - 2P_{BCB} + 2P_{ABA} \right)}\)
证毕

hbghlyj

回复 2# ellipse
公式中的字母和括号都叠在一起了,如何解决呢

乌贼

题一

$ CI $交圆于$ D $，实则就是证明$ AB，DN，MI $三线共点。

乌贼

回复 4# 乌贼
如图：
延长$ CI $交圆于$ D $，延长$ BI $交圆于$ E $，$ F $为$ AB $与$ DN $交点。知$ NDIE $为平行四边形，$ NDBE $为等腰梯形。
下面证明$ F，I，M $三点共线。易知\[ \angle BIM=\angle DIN\\DB=DI=EN \\DN=IE=EC\\\triangle FDB\sim \triangle NEC \riff DI^2=DF\cdot DN\\\riff\triangle IFD\sim \triangle NID\riff \angle \angle DIE=\angle DNI=\angle NIE\]所以\[ \angle EIF=\angle NID=\angle BIM \]因此$ F，I，M $三点共线。
综上有\[ \angle \angle NIC+\angle BIM=\angle FIB+\angle BIM=180\du  \]

乌贼

题3与题1有关联

乌贼

回复 6# 乌贼
题3就是题1的加强版。
如图：
证明$ MI，AC，KQ $三线共点即$ E，N，I，M $四点共线。
由\[ \triangle EQC\sim \triangle CQK \]可推出（有点复杂）\[ \triangle EKN\sim \triangle IQK\riff \triangle EKN\sim \triangle IPN \riff \angle ENK=\angle INP \]故$ E，N，I，M $四点共线。再证明$ AE=DF $应该不难……

hbghlyj

以下结论可能有用

题1中设BC上的内切圆切点为F,对ABFC用牛顿定理(因AB+CF=AC+BF)得AF中点在IM上.

见2600第一节的1(4楼)

hbghlyj

第二题.设过A的高线与过F的DE垂线交于K.
设J是A所对的旁心,由对边平行得AJFK是平行四边形,则KJ平分AF.
由8#的结论得KJ平分BC.证毕!

乌贼

链接：forum.php?mod=viewthread&tid=4714&highlight=
         forum.php?mod=viewthread&tid=7370

乌贼

回复 7# 乌贼
接7楼
如图：
$ L $为$ DI，CK $延长线交点。有\[ \angle AIL=\angle ACL=\angle 1 \]即$ AICL $且圆心为$ Q $得\[ \angle QLC=\angle QCL=\angle QEC \]故$ LQCE $四点共圆因此\[ EL\px FC \]所以$ ELDF $为矩形。又\[ \triangle AEQ\cong \triangle LEQ\riff \\AE=EL=DF \]

乌贼

与题6串一串：forum.php?mod=viewthread&tid=5555&highlight=
                   forum.php?mod=viewthread&tid=4111&hig … 上中点与对应内切圆切点连线，求证角平分线

乌贼

回复 10# hbghlyj
4,5题留给你。题6
如图：
延长$ FE，PQ $交于点$ H $，连接$ I_AH $分别交$ \triangle AEF $外接圆于$ L $。
先证$ ADKL $四点共线。由$ DMI_AH $四点共圆得\[ \angle I_AHM=\angle MDI_A  \]又\[ I_AM\cdot AI_A=I_AF^2=DI_A^2\\\riff\triangle DMI_A\sim \triangle ADI_A\\\angle I_AAD=\angle MDI_A= \angle I_AHM\\\riff AD\perp I_AH  \]所以$ ADKL $四点共线。
因$ MKLI_A $四点共圆。有\[ HQ\cdot HP=HL\cdot HI_A=HK\cdot HM \]得$ PQKM $四点共圆即\[ \angle PMF=\angle PQK \]
设$ G $为$ EF $与$ PI_A $交点，延长$ AG $交$ \triangle AEF $外接圆于$ N $。由$ APGM $四点共圆，故\[ \angle PAN=\angle PMF=\angle PQK \]得$ QKN $三点共线。
由$ MGNI_A $四点共圆，得\[ \angle GMN=\angle GI_AM=\angle PAN=\angle PMG \\\angle MNG=\angle MI_AG=\angle PNG\]由三角形平分线原理知\[ \angle MPG=\angle I_APN=\angle NQI_A=\angle KQI_A \]

乌贼

回复 14# 乌贼
此题难就难在证明$ QKN $三点共线（不知梅氏能否轻松搞定），思考中又被$
PMKQ $四点共圆卡住了……最后终于通过添加多条辅助线并构造三角形$ PI_AH $搞定。

乌贼

题5

$ GF $与$ PI_A $的交点为$ Q $，实质就是证明$ ADQK $四点共线。

乌贼

回复 15# 乌贼
把它证完整。
如图：
  先证$ ADQ $三点共线，连接$ AI_A，AQ，PM，MI_A，PK，MK $，因为$ AMQP $及$ PMI_AK $四点共线。有\[ \angle MAQ=\angle MPQ=\angle MKI_A \]连接$ ID $，作$ IN\perp AC $，垂足为$ N $。有\[ \angle AID=\angle MI_AK\\\dfrac{AI}{ID}=\dfrac{AI}{IN}=\dfrac{AF}{AM}=\dfrac{GI_A}{MI_A}=\dfrac{MI_A}{I_AK }\]得\[ \triangle AID\sim \triangle KI_AM\\\riff \angle IAD=\angle MKI_A=\angle MAQ \]所以$ ADQ $三点共线。
再证$ ADK $三点共线。同理\[ \angle AID=\angle MI_AK \\\dfrac{AI}{ID}=\dfrac{AI_A}{I_AK}\\\riff \triangle AID\sim \triangle AI_AK\\\riff \angle IAD=\angle I_AAK \]即$ ADK $三点共线。
因此$ ADQK $四点共线。
设$ AK $交圆$ I_A $于$ J $。有\[ \angle I_APK=\angle I_AMK=\angle I_AAK+\angle MKA=\angle MKI_A+\angle MKA=\angle I_AKJ=\angle I_AJK \]所以$ PJMI_AK $五点共圆。得\[ \angle JPI_A=\angle JKI_A \]连接$ EJ $并延长交$ PI_A $于$ H $。有$ APHJ $四点共圆。故\[ \angle JAH=\angle JPH=\angle JKI_A\\\riff AH\px EK\\\riff AH\perp DE \]证毕

乌贼

回复 9# hbghlyj
只剩题4，该你出手了。

hbghlyj

以下结论可能有用

ABC内接于DEF和PQR,若AD,BE,CF共点,AP,BQ,CR共点,则EQ,FR,BC共点.
这个结论可见于5000的70楼

乌贼

回复 1# ellipse
题4有更一般情况。
如图：
$ \triangle ABC $内切圆$ I $对应边$ BC，CA，AB $上的切点分别为$ D，E，F $。过点$ C $的直线分别交$ FE，FD $的延长线于$ N，M $。求证：$ IM\perp BN，AM\perp IN $，且$ DE，AM，BN $三线共点。
只是还是做不出

hbghlyj

题4（forever豪3)
只需证$AI_D,BI_E,CI_F$形成的三角形关于内切圆自极。关于内切圆配极后，等价于如下命题(重新标了字母)：
$I_1,I_2,I_3$是旁心,M,N是弧ABC,ACB的中点,D,E,F是外接圆切线的交点,BDF∩$CNI_1I_2$=G,CDE∩$BMI_1I_3$=H,求证GH,MN,BC,$EI_2,FI_3$共点.
证明:由18#得BC,$EI_2,FI_3$共点.
对于$I_3F$∪$I_2CNI_1G$∪ECHD,$I_2E∪I_1HMBI_3$∪BDFG,GH∪$I_1I_2I_3DEF$用Cayley-Bacharach定理得GH,$EI_2,FI_3$共点.

对于BC$\cup I_2CNI_1G\cup I_1HMBI_3$,MN∪ECHD∪BDFG,GH∪ABCMN用Cayley-Bacharach定理得BC,MN,GH共点.

得证.
注1:其中ABCMN指外接圆,$I_1I_2I_3DEF$指Stammler双曲线,其他的字母组合均指直线.
注2:本题的图形中可以找到两组适合Cayley-Bacharach定理的退化三次曲线,都在证明中被用到了.直接观察很难配出这种复杂的定理,所以最好交给机器去做,MMA代码见这里.