四点共圆

大佬最帅

用复数是不是好证一些

战巡

回复 1# 大佬最帅

各种连线如图


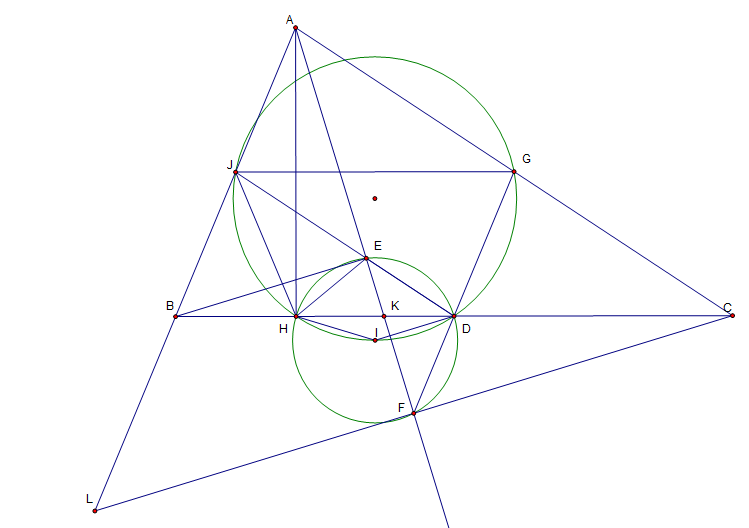
首先这里延长了$AB$和$CF$，交于$L$，显然会有$AL=AC, LF=CF$，于是$DF$就是$\Delta CBL$中位线，有$DF\parallel BL$，也就是$F,D,G$共线。
如果令$J$为$AB$中点，同理也会得到$J,E,D$共线。
不但如此，还会得到$DF=DE=\frac{1}{2}(AC-AB)$，以及$\angle DEF=\angle DFE=\angle BAE=\angle CAF$

这里连一下$HF$，则有$\angle FHD=\angle FED=\angle CAF$，故此$A,H,F,C$共圆，而后有$\angle AHC=\angle AFC=90\du$，于是同样会有$A,E,H,B$共圆。

接下来我们来证明$J,H,I,D,G$这5个点共圆

首先$\Delta JGD$其实就是三个中点连成的三角形，很显然会有$\angle JGD=\angle ABC$
另外由于$\angle AHB=90\du$，$J$为$AB$中点，可得$JH=JB$，会有$\angle JHB=\angle JBH=\angle JGD$，故此$J,H,D,G$共圆。

另一方面，易证$\angle HID=2(180\du-\angle HED)$，而$\angle HED=\angle HEK+\angle DEK=\angle ABH+\angle BAE$，$180\du-\angle HED=180\du-\angle ABH-\angle BAE=\angle AKB$
因此$\angle HID=2\angle AKB=2(\angle ACB+\angle BAF)=2\angle ACB+\angle BAC=180\du-\angle ABC+\angle ACB$
而$\angle HJD=180\du-\angle JHD-\angle JDH=\angle JHB-\angle JDB=\angle ABC-\angle ACB$
于是就有$\angle HJD+\angle HID=180\du$，故此$J,H,I,D$共圆

这就完事了

青青子衿

用复数是不是好证一些
大佬最帅 发表于 2022-1-28 21:33

复数$z_1$,$z_2$,$z_3$,$z_4$在同一圆周上或是同一直线上的条件是
\[ \operatorname{Im}\left[\dfrac{(z_1-z_4)(z_3-z_2)}{(z_1-z_2)(z_3-z_4)}\right]=0 \]

isee

回复 2# 战巡

五点共圆了哇~~

TSC999

这种题目确实用复数法证明比较简单。证明方法说明如下：

上述各点的复数坐标是如何算出来的？其实非常简单，只须套用几个推导出来的通用公式即可。例如由不共线的三点求其外接圆圆心坐标的公式；由一点向一直线作垂线，求垂足坐标的公式； 求两条直线交点坐标的公式。。。。。。

hbghlyj

和上次这帖相同