求参数的值,使二元多项式在$ℝ$上可约

hbghlyj

求$k∈ℝ$$$f(x,y)=(x^2+y^2-1)((x-3)^2+y^2-1)+kxy$$在$ℝ$上可约.
$f$在$ℝ$上可约,可以理解为曲线$f$为两条曲线之并,那么这两条曲线的交点(可以是虚的)是$f$的奇点,所以$f=∂_xf=∂_yf=0$.
但是,反过来不正确,比如双纽线$(x^{2}+y^{2})^{2}=2a^{2}(x^{2}-y^{2})$有奇点(0,0)但是不可约.

1. f = (x^2 + y^2 - 1) ((x - 3)^2 + y^2 - 1) + k x y;
2. N[Assuming[k∈Reals, Solve[D[f, x] == D[f, y] == f == 0, {k, x, y}]]]

复制代码

输出:
{{k -> 0., x -> 1.5, y -> 0. - 1.11803 I},
{k -> 0., x -> 1.5, y -> 0. + 1.11803 I},
{k -> -3.03948, x -> 1.3361, y -> 0.613914},
{k -> 3.03948, x -> 1.3361, y -> -0.613914}}
验证:
$k=0$时,$f=(x^2+y^2-1)((x-3)^2+y^2-1)$

$k=3.03948$时,有奇点,但是不可分解
$k=-3.03948$时,有奇点,但是不可分解

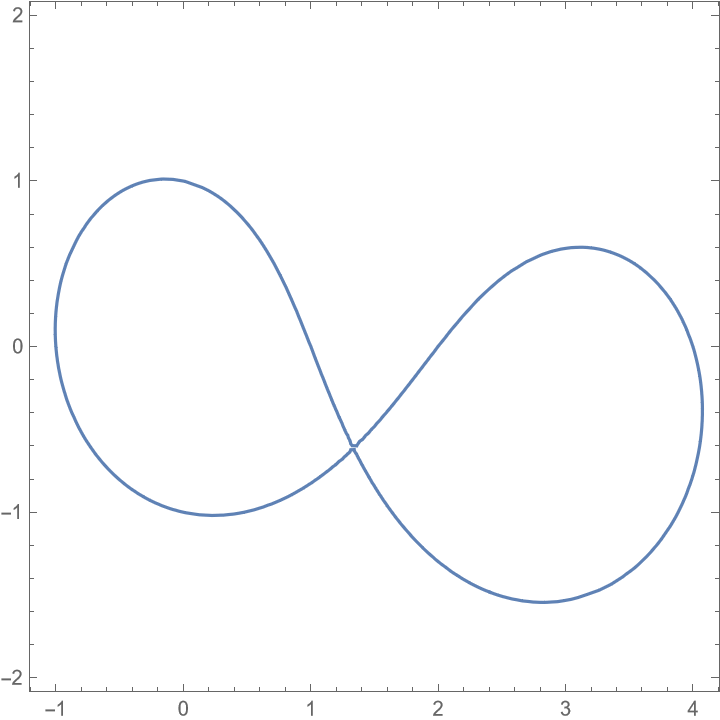
所以只有$k=0$时可分解.

hbghlyj

对任意正整数$n$,是否存在二元多项式$f(x,y),g(x,y)$,使得,恰存在$n$个实数$k$使$f(x,y)+k\ g(x,y)$可分解,且$f(x,y),g(x,y)$不是一元多项式.

比如1楼是$n=1$,只有$k=0$时可分解.
只要稍微改一下:$(x^2 + y^2 - 1) ((x - 3)^2 + y^2 - 1) + k\left(x y-(x^2 + y^2 - 1) ((x - 3)^2 + y^2 - 1)\right)$
就得到$n=2$的例子,只有$k=0,1$时可分解,因为$xy=0$可以分成$x=0$和$y=0$.
$n=3$呢?