平行于角平分线的直线交四边于四点，证张角相等

kuing

如下图，`AK` 是 `\odot O` 的直径，`B`, `C` 是圆上两点，过 `O` 作一直线 `l` 使之平行于 `\angle BAC` 的角平分线，`l` 与直线 `BA`, `AC`, `CK`, `KB` 分别交于 `D`, `E`, `F`, `G`，则有 `\angle EBF=\angle DCG`。

注：
问题源自：forum.php?mod=viewthread&tid=9039
原题较繁，我将其分解为两部分，以上命题为其一。
原帖楼主已经用复平面解析几何法证出，但尚未得到几何证法，而原帖在软件区，故重新发布于这边。

乌贼

如图：
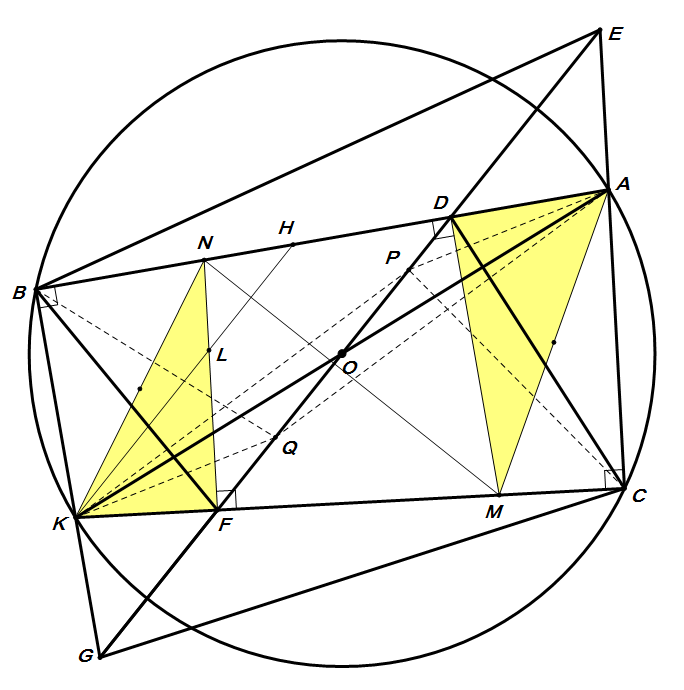
先证\[ \angle KBF=\angle ACD \]
作$ FN\px AC $交$ AB $于$ N $，$ DM\px BK $交$ CK $于$ M $，作$ KH\px EG $分别交$ FN,AB $于$ L,H $。有$ KBNF,FNDM,MDAC $三组四点共圆，得\[ \angle DMN=\angle DFN=\angle FLK\riff \triangle LFK\sim \triangle MDN\riff \dfrac{FL}{FK}=\dfrac{DM}{DN} \]又\[ \angle NDF=\dfrac{1}{2}\angle BAC=\dfrac{1}{2}\angle BNF\riff FN=ND \]又有\[ FL=DH=DA \]所以有\[ \dfrac{DA}{FK}=\dfrac{DM}{FN}\riff \triangle NFK\sim \triangle MDA\riff \angle KBF=\angle KNF=\angle DMA=\angle ACD \]
再证\[ \angle ABE=\angle KCG \]分别取$ AF,DG $中点$ P,Q $，有\[ \angle DBQ=\angle BDQ=\angle ADE=\angle AED=\angle ACP \]故$ AQBE $四点共圆，$ ADPMC $五点共圆
同理$ KPCG $四点共圆，$ BNQFK $五点共圆,因此\[ \angle APD=\angle ACD=\angle KBF=\angle KQG\riff \triangle AOP\cong \triangle BOQ \]即$ APKQ $为平行四边形，所以\[ \angle ABE=\angle AQE=\angle KPG=\angle KCG \]综上得\[ \angle EBF=\angle DCG \]