|
|
世界著名平面几何经典著作钩沉: 几何作图专题卷. 上(Library Genesis)
反演原理之用途，有一优美之例，即下述Apollonius问题之简单几何解法。
对任一心之反演，Apollonius三圆问题，可化成他三圆之相当问题。(何故如此？)
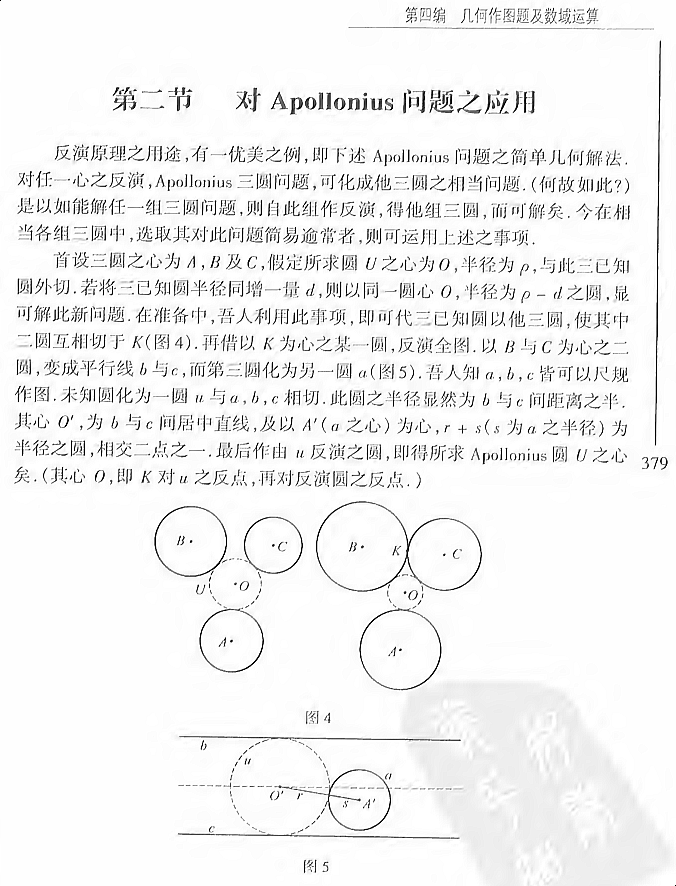
是以如能解任一组三圆问题，则自此组作反演，得他组三圆，而可解矣。今在相当各组三圆中，选取其对此问题简易逾常者，则可运用上述之事项。首设三圆之心为A,B及C，假定所求圆U之心为O，半径为ρ，与此三已知圆外切。若将三已知圆半径同增一量d，则以同一圆心O，半径为ρ-d之圆，显可解此新问题。在准备中，吾人利用此事项，即可代三已知圆以他三圆，使其中二圆互相切于K(图4)。再借以K为心之某一圆，反演全图。以B与C为心之二圆，变成平行线b与c，而第三圆化为另一圆a(图5)。吾人知a,b,c皆可以尺规作图。未知圆化为一圆u与a,b,c相切。此圆之半径r显然为b与c间距离之半。其心O'，为b与c间居中直线及以A'(a之心)为心，r+s(s为a之半径)为半径之圆，相交二点之一。最后作由u反演之圆，即得所求Apollonius圆U之心矣。(其心O，即K对u之反点，再对反演圆之反点。) |
|
hbghlyj
Posted 2022-6-5 12:24
