stereographic projection

hbghlyj

pi.math.cornell.edu/~boyang/2220%20s2017/math2220_notes/notes_sec_2.1.pdf
$S: \mathbb{R}^{2} \rightarrow S \backslash\{N\}$ has the formula: $$ S(x, y)=(X, Y, Z)=\left(\frac{2 x}{x^{2}+y^{2}+1}, \frac{2 y}{x^{2}+y^{2}+1}, \frac{x^{2}+y^{2}-1}{x^{2}+y^{2}+1}\right) $$

It is not hard to show that $S$ has an inverse function $F: S \backslash\{N\} \rightarrow \mathbb{R}^{2}$ : $$ F(X, Y, Z)=(x, y)=\left(\frac{X}{1-Z}, \frac{Y}{1-Z}\right) \text {. } $$

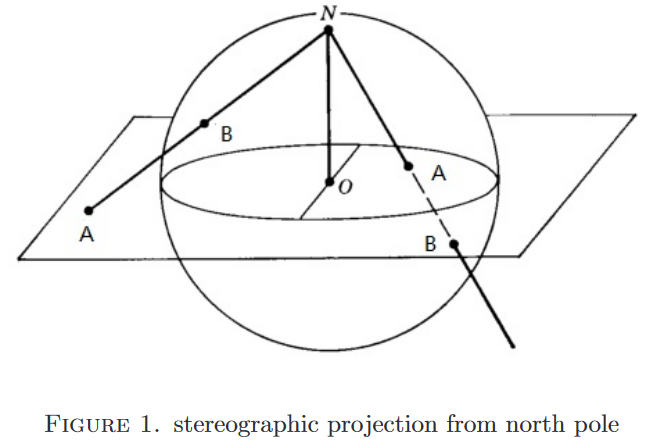
	PROOF. The general point on the line joining $z$ and $N$ is $t(0,0,1)+(1-t)(x, y, 0)$. There is a unique value of $t$ for which this point lies on the sphere, namely $t=\left(x^{2}+y^{2}-1\right) /\left(x^{2}+y^{2}+1\right)$, as can be easily checked. Remark This can be written as$$S(z)=\frac{1}{1+|z|^{2}}\left(2 \Re(z), 2 \Im(z),|z|^{2}-1\right)$$
	We have identified $\mathbb{C}$ with $\mathbb{S} \backslash\{N\}$ by stereographic projection. $\mathbb{S} \backslash\{N\}$ has a natural metric: the one induced from the Euclidean metric on $\mathbb{R}^{3}$. This induces a metric on $\mathbb{C}$, which we call $d$. To spell it out, $$ d(z, w):=\|S(z)-S(w)\| . $$ LEMMA For any $z, w \in \mathbb{C}$ we have $$ d(z, w)=\frac{2|z-w|}{\sqrt{1+|z|^{2}} \sqrt{1+|w|^{2}}} $$
	Since $\|S(z)\|=\|S(w)\|=1$ we have $$ \|S(z)-S(w)\|^{2}=2-2\langle S(z), S(w)\rangle . $$ Using the formulae, $$ \langle S(z), S(w)\rangle=1-\frac{2|z-w|^{2}}{\left(1+|z|^{2}\right)\left(1+|w|^{2}\right)} . $$ Therefore $$ \|S(z)-S(w)\|^{2}=\frac{4|z-w|^{2}}{\left(1+|z|^{2}\right)\left(1+|w|^{2}\right)} $$ as required.

hbghlyj

Using the formulae,$$\langle S(z), S(w)\rangle=1-\frac{2|z-w|^{2}}{\left(1+|z|^{2}\right)\left(1+|w|^{2}\right)} .$$

In detail:
\begin{align*}
\langle S(z), S(w)\rangle
&=\left<\frac{1}{1+|z|^{2}}\left(2 \Re(z), 2 \Im(z),|z|^{2}-1\right),\frac{1}{1+|w|^{2}}\left(2 \Re(w), 2 \Im(w),|w|^{2}-1\right)\right>\\
&=\frac{4\Re(z)\Re(w)+4\Im(z)\Im(w)+(|z|^2-1)(|w|^2-1)}{\left(1+|z|^{2}\right)\left(1+|w|^{2}\right)}\\
&=\frac{4\Re(z\bar w)+(|z|^2-1)(|w|^2-1)}{\left(1+|z|^{2}\right)\left(1+|w|^{2}\right)}\\
&=\frac{2(z\bar w+\bar zw)+(|z|^2-1)(|w|^2-1)}{\left(1+|z|^{2}\right)\left(1+|w|^{2}\right)}\\
&=\frac{2\left(|z|^2+|w|^2-|z-w|^2\right)+(|z|^2-1)(|w|^2-1)}{\left(1+|z|^{2}\right)\left(1+|w|^{2}\right)}\\
&=1-\frac{2|z-w|^{2}}{\left(1+|z|^{2}\right)\left(1+|w|^{2}\right)}
\end{align*}

hbghlyj

complex.pdf Example 2.6

Let $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ be given by $f(z)=\frac1z(z ≠ 0, \infty)$ and $f(0)=\infty, f(\infty)=0$. One can check that if $S(z)=(t, u, v) \in \mathbb{S}$ then $S(f(z))=(t,-u,-v)$. That is, under the identification $S: \mathbb{C}_{\infty} \rightarrow \mathbb{S}, f$ corresponds to the (obviously continuous) map $(t, u, v) \mapsto(t,-u,-v)$, that is to say rotation by $\pi$ about the $x$-axis.