几何等比数列

dlsh

非线性构造，难

hbghlyj

小结论.

若$A_0,B_0,C_0,D_0$与$A_1,B_1,C_1,D_1$是楼主所说的“几何等比数列”, 则$A_0B_1\cap A_1B_0,B_0C_1\cap B_1C_0,C_0D_1\cap C_1D_0,A_0D_1\cap A_1D_0$共线.
反过来, 若$A_0B_1\cap A_1B_0,B_0C_1\cap B_1C_0,C_0D_1\cap C_1D_0,A_0D_1\cap A_1D_0$共线, 则$A_0,B_0,C_0,D_0$与$A_1,B_1,C_1,D_1$等比.

hbghlyj

这样一来, 由前两个等比得$AD,BE,CF$三线共点且$PO,QM,RN$三线共点, 所以得到第三个是等比.

hbghlyj

如图, 两条红色直线$L_0,L_1$的并是(退化的)二次曲线$\Gamma$, 点$A_0,A_1$是定点, 对于直线$L_0$上的点$P_0$, 我们将它对应到$\Gamma$上的点$P_1$使$P_0A_1\cap P_1A_0$在定直线上, 则$P_0\mapsto P_1$是$L_0\to L_1$的一个射影变换[或者可视为$\Gamma\to\Gamma$的一个对合]
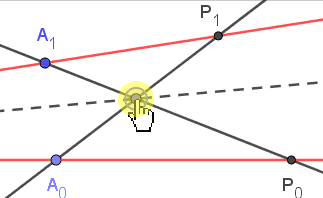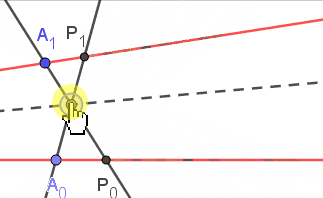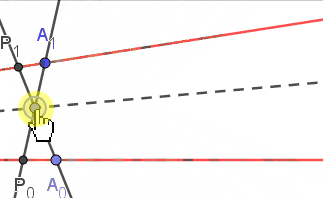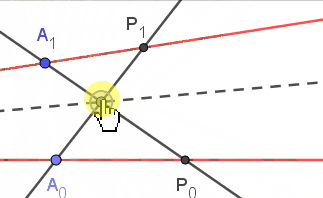
如图, 点$A_0,B_0;A_1,B_1$是两条直线上的定点, 对于$L_0$上的点$P_0$, 把它映射到直线$L_1$上的$P_1$, 使$A_0B_0:B_0P_0=A_1B_1:B_1P_1$, 则$P_0\mapsto P_1$也是$L_0\to L_1$的一个射影变换
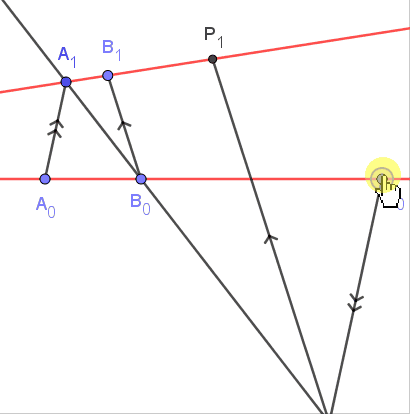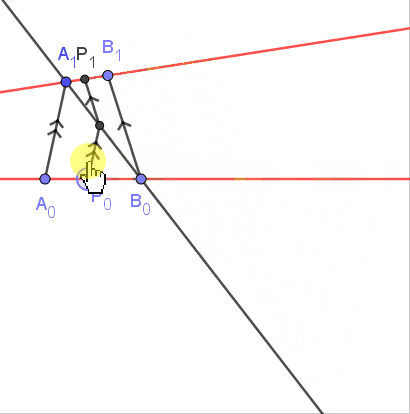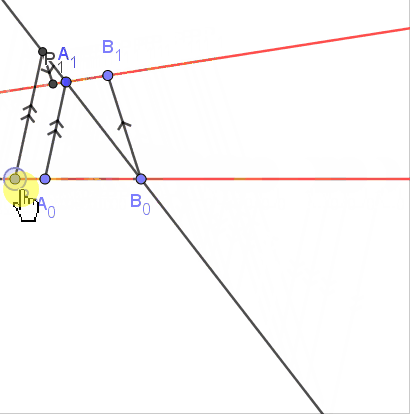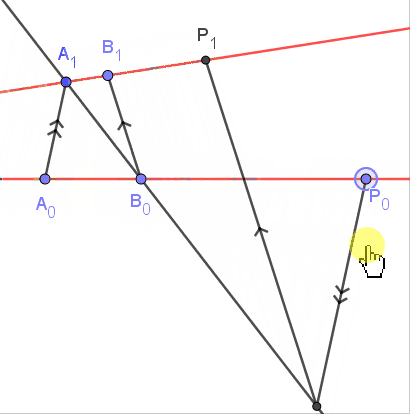
上述两个射影变换都把$A_0,B_0,C_0$映射为$A_1,B_1,C_1$, 根据Fundamental Theorem, 这两个变换相等.

The Fundamental Theorem

Let l and l' be two distinct lines in a projective plane with A,B,C on l and A',B',C' on l'. Then there is one and only one projectivity of l onto l' such that ABC ^ A'B'C'.

Fundamental theorem of projective geometry

Given two projective frames of a projective space P, there is exactly one homography of P that maps the first frame onto the second one.

交比与射影对应

定义1.9:设f是二次曲线$\Gamma$上的射影变换,取$\Gamma$上一定点U(U$\ne f(U)$)
设P是$\Gamma$上的动点Pf(U)与Uf(P)的交点轨迹是一条不依赖U选取的直线,称为f关于二次曲线$\Gamma$的射影轴.
f为两个对合的复合,则两个对合中心的连线是f的射影轴.所以,f的射影轴与二次曲线的交点是f的不动点.

Ly-lie

hbghlyj 发表于 2022-11-11 17:27
小结论.

若$A_0,B_0,C_0,D_0$与$A_1,B_1,C_1,D_1$是楼主所说的“几何等比数列”, 则$A_0B_1\cap A_1B_0,B_ ...

这个结论应该不对，因为题目中的线段比相等要比交比相等更“强”，而三点共线只能保证交比相等，不能保证等比，故不是充要条件（只要两个三角形内接于同一圆锥曲线，就有层主所说的性质成立，这由彭赛列闭合定理保证）

hbghlyj

Two Triangles Inscribed in a Conic - with Solution
看到一个5#相同的图