垂足曲线的法线

hbghlyj

$B$是圆上的动点, $C$是$A$在$B$处的切线上的投影, $M$是$AB$中点,求证$CM$是$C$的轨迹的法线.
又见Limaçon  蚶线  Pedal curve #Example
相关问题:Prove that the locus is tangent to the circle

kuing

很简单，而且具有一般性，圆可以改为任意光滑曲线。

当 `B` 运动时，由于切线和垂线要保持垂直，所以两者的角速度相同，设 `C` 的速度为 `v`，如下图所示：

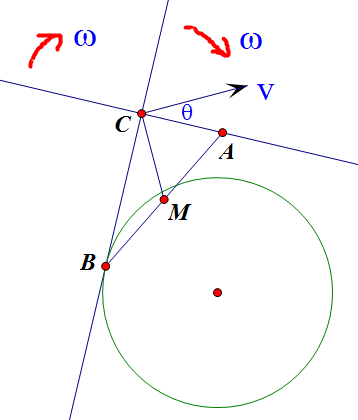
则有
\begin{align*}
v\sin\theta&=\omega\cdot AC,\\
v\cos\theta&=\omega\cdot BC,
\end{align*}
相除得
\[\tan\theta=\frac{AC}{BC}=\tan\angle ABC=\tan\angle MCB,\]
所以 `\theta=\angle MCB`，所以 `v` 与 `MC` 垂直，因此 `CM` 就是 `C` 的轨迹的法线。