|
|
敌舰逆时针沿着以(2,0)为中心$1$为半径的圆航行, 速率恒为$2\pi\over3$.
从(0,0)发射一枚鱼雷, 速率恒为$\sqrt3$, 击中敌舰的最短时间?
解:
设发射时刻为0.
为了击中敌舰的时间最短, 让鱼雷方向始终指向敌舰, 此时相对速度最大, 也就是和目标的距离减少最快.
\begin{aligned}
y'(t)&=\frac{\sqrt{3} \left(\sin \left(\frac{2 \pi t}{3}\right)-y(t)\right)}{\sqrt{\left(\sin \left(\frac{2 \pi
t}{3}\right)-y(t)\right)^2+\left(2+\cos \left(\frac{2 \pi t}{3}\right)-x(t)\right)^2}} \\
x'(t)&=\frac{\sqrt{3} \left(2+\cos \left(\frac{2 \pi t}{3}\right)-x(t)\right)}{\sqrt{\left(\sin \left(\frac{2 \pi
t}{3}\right)-y(t)\right)^2+\left(2+\cos \left(\frac{2 \pi t}{3}\right)-x(t)\right)^2}} \\
x(0)&=y(0)=0
\end{aligned}使用NDSolve
- ClearAll[x,y];{x,y}=Last/@Evaluate[NDSolve[{y'[t]==Sqrt[3] (Sin[2Pi/3 t]-y[t])/Sqrt[(Sin[2Pi/3 t]-y[t])^2+(2+Cos[2Pi/3 t]-x[t])^2],x'[t]==Sqrt[3] (2+Cos[2Pi/3 t]-x[t])/Sqrt[(Sin[2Pi/3 t]-y[t])^2+(2+Cos[2Pi/3 t]-x[t])^2],x[0]==y[0]==0},{x,y},{t,0,1}][[1]]];
- t0=t/.FindRoot[EuclideanDistance[{x[t],y[t]},{2,0}]==1,{t,.3}];
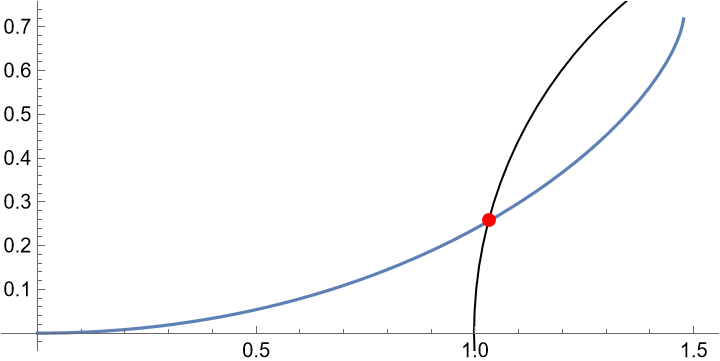
- Show[ParametricPlot[{x[t],y[t]},{t,0,1}],Graphics[{Circle[{2,0},1],Red,PointSize[Large],Point[{x[t0],y[t0]}]}]]
| (图中红点)击中时刻$t_0\approx0.621934$ |
|
其他轨迹如果能击中, 击中时间只会更长, 例如, 沿直线从(0,0)到$(\frac32,\frac{\sqrt3}2)$将在时刻$1$击中敌舰. |
|