日出引理

hbghlyj

Rising sun lemma
连续函数 $g:[a,b]\toℝ$，$S$ 是 $[a,b]$ 中 $x$ 的集合，使得存在 $y∈(x,b]$ 且 $g(y) > g(x )$.（注意 $b$ 不能在 $S$ 中，尽管 $a$ 可能在。）

定义 $E = S ∩ (a,b)$。则它可以写成 $$E=\bigcup _{k}(a_{k},b_{k})$$ 使得 $g(a_k) = g(b_k)$，除非对于某个 $k$，$a_k = a ∈ S$，在这种情况下，对于那个 $k$，$g(a) < g(b_k)$。 此外，如果 $x ∈ (a_k,b_k)$，则 $g(x) < g(b_k)$。

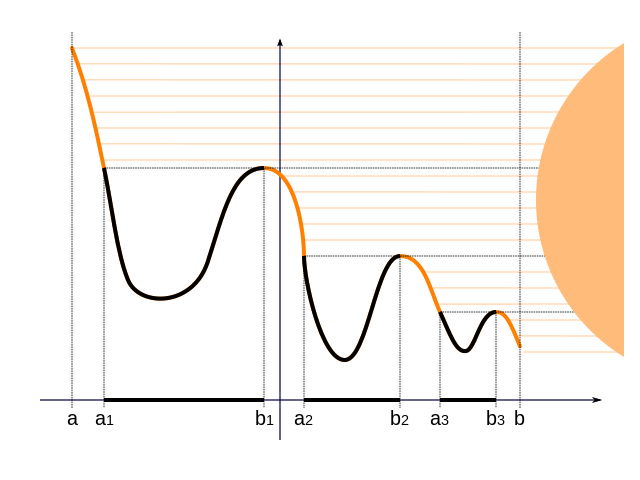
从图象看，定理是说，黑色集合可以分成小区间，函数在左端点处的值等于右端点处的值。

我们需要一个引理：假设 $[c,d) ⊂ S$，但 $d ∉ S$。那么 $g(c) < g(d)$。

证明

假设 $g(c) ≥ g(d)$。则 $g$ 在 $[c,d]$ 上的某个点 $z < d$ 达到最大值。由于 $z ∈ S$，在 $(z,b]$ 中存在一个 $y$，且 $g(z) < g(y)$。如果 $y ≤ d$，则 $g$ 在 $[c,d]$ 上不会在 $z$ 处达到最大值。因此，$y ∈ (d,b], g(d) ≤ g(z) < g(y)$。这意味着$d ∈ S$，这是矛盾的，因此引理成立。

集合 $E$ 是 $ℝ$ 中的开集，因此所以它可以写成可数个不相交区间 $(a_k,b_k)$ 的并集。

从引理可以直接得出 $g(x) < g(b_k)$ 对 $x ∈ (a_k,b_k)$。由于 $g$ 是连续的，还必须满足 $g(a_k) ≤ g(b_k)$。
如果 $a_k ≠ a$ 或 $a ∉ S$，则 $a_k ∉ S$，因此 $g(a_k) ≥ g(b_k)$，否则 $a_k ∈ S$。因此，在这些情况下，$g(a_k) = g(b_k)$。
最后，如果 $a_k = a ∈ S$，引理告诉我们 $g(a) < g(b_k)$。

kuing

forum.php?mod=viewthread&tid=8017