复平面上解析几何构图法例子

TSC999

  构 图 方 法 （1）

字母上面有一横线者表示共轭复数。 变量 \(u \)、 \(v \) 均为单位复数，因此 \(\overline{u}=1/u\)，\(\overline{v}=1/v\)。


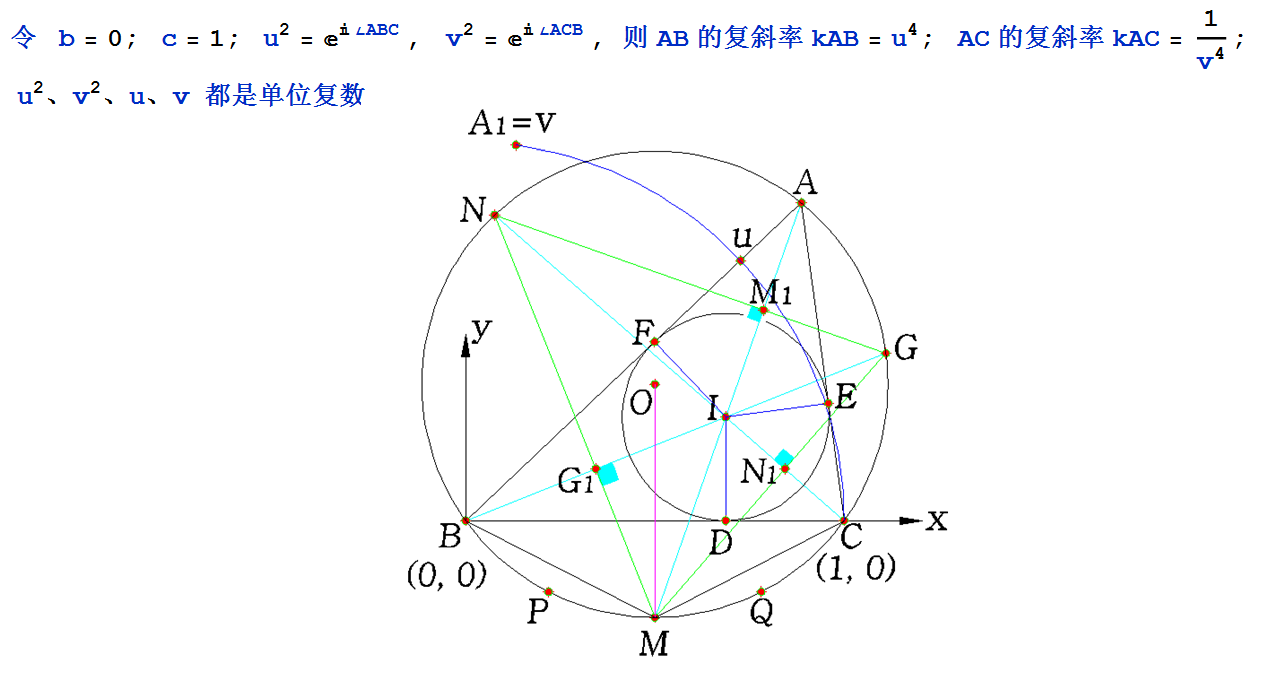
此时各点复坐标如下（推导过程略去）：

1.     ①  AB 的复斜率 kAB = u^4;  AC 的复斜率 kAC = 1/v^4;  MN是BI的垂直平分线; MG是CI的垂直平分线; GN是AI的垂直平分线;  即  IG1 = G1B;  IN1 = N1C;  IM1 = M1A;
2.   ②  \!\(\*OverscriptBox[\(o\), \(_\)]\) = o = 0; \!\(\*OverscriptBox[\(c\), \(_\)]\) = c = 1; a = (u^4 (v^4 - 1))/( u^4 v^4 - 1);
3. \!\(\*OverscriptBox[\(a\), \(_\)]\) = (v^4 - 1)/(u^4 v^4 - 1);   
4.   ③  \[EmptyUpTriangle]ABC 的外心坐标  o = (u^4 v^4)/(u^4 v^4 - 1); \!\(\*OverscriptBox[\(o\), \(_\)]\) = 1/(1 - u^4 v^4);
5. 外接圆半径 R = ( I u^2 v^2)/(u^4 v^4 - 1)。
6. ④ \[EmptyUpTriangle]ABC 的内心坐标  i = (u^2 (v^2 - 1))/(u^2 v^2 - 1); \!\(\*OverscriptBox[\(i\), \(_\)]\) = (v^2 - 1)/(u^2 v^2 - 1);  内切圆半径 r = (I (u^2 - 1) (v^2 - 1))/(2 (1 - u^2 v^2));
7. ⑤ 对偶 \[EmptyUpTriangle]MGN 各顶点坐标：  m = (u^2 v^2)/(u^2 v^2 - 1);  \!\(\*OverscriptBox[\(m\), \(_\)]\) = 1/(1 - u^2 v^2);   n = (u^4 (v^2 - 1) v^2)/(u^4 v^4 - 1);   \!\(\*OverscriptBox[\(n\), \(_\)]\) = (v^2 - 1)/(u^4 v^4 - 1);
8. g = (u^2 (u^2 v^4 - 1))/(u^4 v^4 - 1);  \!\(\*OverscriptBox[\(g\), \(_\)]\) = (u^2 v^4 - 1)/(u^4 v^4 - 1);
9. ⑥ 切点 D、E、F 的坐标： d = ((u^2 + 1) (v^2 - 1))/(2 u^2 v^2 - 2);  \!\(\*OverscriptBox[\(d\), \(_\)]\) = ((u^2 + 1) (v^2 - 1))/(  2 u^2 v^2 - 2);  e = ((v^2 - 1) (2 u^2 v^2 + u^2 - 1))/(2 v^2 (u^2 v^2 - 1));     \!\(\*OverscriptBox[\(e\), \(_\)]\) = ((v^2 - 1) ((u^2 - 1) v^2 - 2))/(2 (1 - u^2 v^2));   f = (u^2 (u^2 + 1) (v^2 - 1))/(2 (u^2 v^2 - 1));  
10. \!\(\*OverscriptBox[\(f\), \(_\)]\) = ((u^2 + 1) (v^2 - 1))/( 2 u^2 (u^2 v^2 - 1));
11. ⑦ 三个垂足 M1、G1、N1 的坐标：m1 = (u^2 (v^2 - 1) (2 u^2 v^2 + u^2 + 1))/( 2 (u^4 v^4 - 1));   
12. \!\(\*OverscriptBox[\(m1\), \(_\)]\) = ((v^2 - 1) (u^2 v^2 + v^2 + 2))/(2 (u^4 v^4 - 1));
13. n1 = (2 u^2 v^2 - u^2 - 1)/(2 ( u^2 v^2 - 1));   \!\(\*OverscriptBox[\(n1\), \(_\)]\) = (u^2 v^2 + v^2 - 2)/( 2 ( u^2 v^2 - 1));  g1 = (u^2 (v^2 - 1))/(2 ( u^2 v^2 - 1));   \!\(\*OverscriptBox[\(g1\), \(_\)]\) = (v^2 - 1)/(2 ( u^2 v^2 - 1));  
14. ⑧ \[EmptyUpTriangle]ABC 的各边长度：BC = 1;  AB = (u^2 (v^4 - 1))/(u^4 v^4 - 1);   AC = v^2(u^4 - 1)/(u^4 v^4 - 1);  
15. AM = (u v (u^2 + v^2) I)/(u^4 v^4 - 1);
16. ⑨  BM 弧的中点 p = ( I u^3 v^3 - u^4 v^4)/(1 - u^4 v^4); \!\(\*OverscriptBox[\(p\), \(_\)]\) = ( 1 + I u v)/( 1 - (u^4) (v^4) );   CM 弧的中点  q = (u^4 v^4 + I u v)/(u^4 v^4 - 1); \!\(\*OverscriptBox[\(q\), \(_\)]\) = (I u^3 v^3 - 1)/(u^4 v^4 - 1);
17.          G1N1 // BC;   M1N1 // AC;   M1G1 // AB;  
18. Subscript[G, 1] I = Subscript[G, 1] B;  
19. Subscript[N, 1] I = Subscript[N, 1] C;  
20. Subscript[M, 1] I = Subscript[M, 1] A;
21. ⑩  九点圆圆心坐标：o9 = (u^4 (v^4 - 1) - 1)/(2 u^4 v^4 - 2);    \!\(\*OverscriptBox[\(o9\), \(_\)]\) = ((u^4 + 1) v^4 - 1)/(
22.   2 u^4 v^4 - 2);

Copy the Code

注： △mng 是 △ABC 的对偶三角形。

TSC999

构 图 方 法（2）

各点复坐标：


注： 变量 \(u \)、 \(v \) 均为单位复数，因此 \(\overline{u}=1/u\)，\(\overline{v}=1/v\)。

TSC999

构 图 方 法 （3）

各点坐标：

TSC999

构 图 方 法 （4）

各点坐标：

TSC999

构 图 方 法 （5）

各点坐标：

TSC999

构 图 方 法 （6）

各点坐标：

TSC999

构 图 法（7）

各点坐标：

TSC999

构 图 法 （8）

各点坐标：

TSC999

构 图 法 （9）

各点坐标:

TSC999

构 图 法（10）

各点坐标:

注：有些点图中没有示出。

uk702

好资料，必需收藏，谢谢。

TSC999

构 图 法 (11)

注：内切圆半径为 1。

TSC999

说明： 每一种构图中，都很容易求出垂心、重心、费尔巴哈点、角平分线与对边的交点、垂线与对边的交点，.........等等各种点的坐标。上面示例中，许多点的坐标没有给出，读者需要时可自行计算。
计算方法见复平面上的解析几何部分公式:
forum.php?mod=viewthread&tid=10421&extra=page=1