$\exp(-n)\sum_{i=0}^nn^i/i!>\frac12$

hbghlyj

$\forall n\ge1$,
$$\exp(-n)\sum_{i=0}^n{n^i\over i!}>\frac12$$
WolframAlpha

kuing

初版论坛有：kuingggg.github.io/5d6d/thread-868-1-1.html
后来也有：kuing.cjhb.site/forum.php?mod=viewthread&tid=3230

hbghlyj

kuing 发表于 2023-6-17 14:20
后来也有：https://kuing.cjhb.site ... thread&tid=3230

如何方便地得到$\sum_{i=0}^\infty (\frac{i-n}{\sqrt{n}})^3\frac{n^i}{i!}e^{-n}=\frac{1}{\sqrt{n}}$
$\iff \sum_{i=0}^\infty (i-n)^3\frac{n^i}{i!}=ne^n$
$f(n)\coloneqq\sum_{i=0}^\infty (i-n)^3\frac{n^i}{i!}$
$f'(n)=\sum_{i=1}^\infty (i-n)^3\frac{n^{i-1}}{(i-1)!}-\sum_{i=1}^\infty (i-n)^2\frac{n^i}{i!}$

hbghlyj

Limit[Exp[-n]Sum[n^(2i)/(2i)!,{i,0,n}],n->oo]
如何证明$\lim_{n\to\infty}\exp(-n)\sum_{i=0}^n{n^{2i}\over(2i)!}=\frac12$
$\sum_{i=0}^\infty{n^{2i}\over(2i)!}=\cosh n$可能有用

hbghlyj

kuing 发表于 2023-6-17 14:20
初版论坛有：https://kuingggg.github.io/5d6d/thread-868-1-1.html

看完这篇文章后，

page68 check that the RHS of (7.1) and (7.2) are the same (for example, either by integrating by parts in (7.2), or by differentiating in (7.1)).\[\frac{e^{-\lambda t}(\lambda t)^{k}}{k !} =\int_{0}^{t} \frac{\lambda^{k} x^{k-1} e^{-\lambda x}}{(k-1) !} d x-\int_{0}^{t} \frac{\lambda^{k+1} x^{k} e^{-\lambda x}}{k !} d x\]

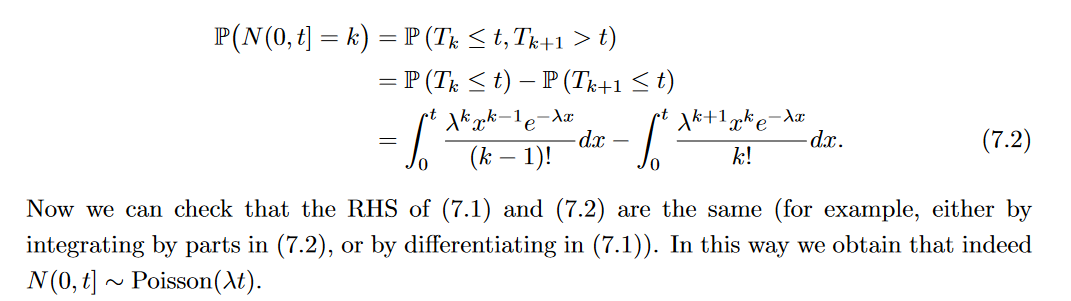
原来这个公式是Taylor公式$f(x)=e^{-\lambda x}$的积分余项$f(x) = f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + \frac{1}{n!}\int_{t=a}^{x}f^{(n+1)}(t)(x-t)^n dt$

LectureNotes2021.pdf page 7