$T$单谱 组成基的特征向量之和为循环向量

hbghlyj

Hoffman & Kuntze, Linear Algebra, page 231

7. Let $V$ be an $n$-dimensional vector space, and let $T$ be a linear operator on $V$. Suppose that $T$ is diagonalizable. (b) If $T$ has $n$ distinct eigenvalues, and if $\{a_1, \dots , a_n\}$ is a basis of eigenvectors for $T$, show that $a = a_1 + \dots + a_n$ is a cyclic vector for $T$.

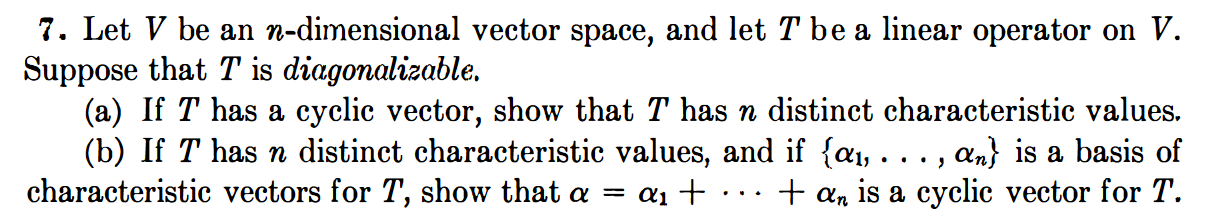
一般地，组成基的广义特征向量之和是一个循环向量？（无论 A 是否可对角化）

1. A=block_diagonal_matrix(jordan_block(1,2),jordan_block(2,2))
2. B=matrix([1,1,1,1]).T
3. C=block_matrix([B,A*B,A*A*B,A*A*A*B],nrows=1)
4. ~C*A*C

复制代码

$A=\left(\begin{array}{rr|rr}
1 & 1 & 0 & 0 \\
0 & 1 & 0 & 0 \\
\hline
0 & 0 & 2 & 1 \\
0 & 0 & 0 & 2
\end{array}\right)$
$B=\left(\begin{array}{r}
1 \\
1 \\
1 \\
1
\end{array}\right)$
$C=\left(\begin{array}{r|r|r|r}B&AB&A^2B&A^3B\end{array}\right)=\left(\begin{array}{r|r|r|r}
1 & 2 & 3 & 4 \\
1 & 1 & 1 & 1 \\
1 & 3 & 8 & 20 \\
1 & 2 & 4 & 8
\end{array}\right)$
$C^{-1}AC=\left(\begin{array}{r|r|r|r}
0 & 0 & 0 & -4 \\
1 & 0 & 0 & 12 \\
0 & 1 & 0 & -13 \\
0 & 0 & 1 & 6
\end{array}\right)$
$x^4-6x^3+13x^2-12x+4=(x - 1)^2 (x -2)^2$

Czhang271828

标题没有 distinct 的条件, 所以不正确. 例如 $I$. 若有 distinct 的条件, 那
\[
\sum_i \lambda _i^0v_i, \sum_i \lambda _i^1v_i, \ldots ,\sum_i \lambda _i^{n-1}v_i
\]线性无关不是明摆着吗. 这组基在 Vdmd 矩阵下变为 $(v_i)_{1\leq i\leq n}$.

hbghlyj

Czhang271828 发表于 2023-6-20 09:54
标题没有 distinct 的条件, 所以不正确.

已修改👌