一道人教四年前的关于圆中比例：1#切线情形 12#割线情形

其妙

将一割线AFD过圆心O，另一割线ABC，C'与C关于AO对称，则有定点E。

比如，让AF=FO，则E为FO中点。 ...
isee 发表于 2014-2-12 23:36

    圆里叫反演吧？   $|OE|\cdot|OA|=r^2$

其妙

设$P(m,0)$，$A$，$B$是椭圆$C:\dfrac{x^2} {a^2}+\dfrac {y^2}{b^2}=1$ 上关于$x$ 轴对称的任意两个不同的点，连结$PB $交椭圆$C $于另一点$E $，则直线$AE$ 与$x$ 轴相交于定点$Q(\dfrac{a^2}{m}，0)$ 。
即：$|OP|\cdot|OQ|=a^2$，特别的，若$P$是“准点”，即$P(\dfrac{a^2}{c},0)$，则定点$Q(c,0)$是焦点。

isee

回复 22# 其妙


    赞！不过，还是感觉圆好玩些……

kuing

bbs.pep.com.cn/thread-342328-31-1.html
601~603#

其妙

回复 24# kuing
准备搞数学空间xycfl的专场了？

删广告专用

回复 25# 其妙
不是，今天lu老帖时看到那帖，顺便发一下来这里

isee

人教 BBS 挂了，把最对味的(主楼)平几证明补上.

---

源自知乎提问


字母如图1所示，用的图1的字母，即有命题：


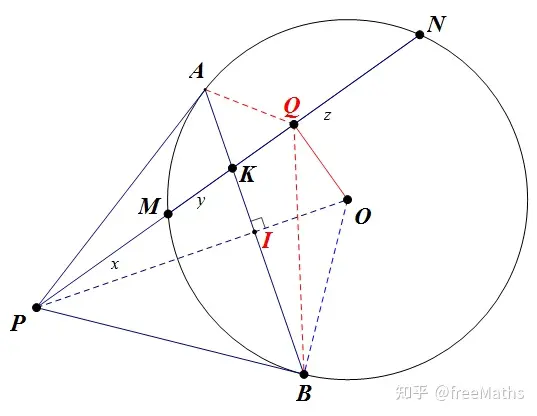
图 1 过点 P 引圆的两切线 A, B 分别为切点

PA,PB为圆O的切线且A,B分别是切点，割线AMN交AB于K，则有PM/MK=PN/NK <=> 1/PM+1/PN=2/PK <=> $y^2+xy+yz-zx=0,$ 其中 x=PM, y=MK, z=KN.

三个 等价结论 全部用 x，y，z 表示并经过简单的计算即知三者是一样的.

图 1 过点 P 引圆的两切线 A, B 分别为切点
由于 $PA,PB$ 是 $\odot O $ 的切线，连接 $OB,OP$ ， $OP$ 交 $AB$ 于 $I,$ 如图1所示，容易证明 $OP\perp AB$ 且 $PB^2=PI\cdot PO.$ (放这里先，别忘记它.)

在割线 $PK$ 上取点 $Q$ 使 $PK\cdot PQ=PB^2(=PM\cdot PN=PA^2),$ 则由 $PK\cdot PQ=PI\cdot PO$ 得 $\color{red}{O,Q,K,I}$ 四点共圆，所以 $OQ\perp MN$ 即点 $Q$ 为 $MN$ 的中点，则由 $PM\cdot PN=PK\cdot PQ\iff x(x+y+z)=(x+y)\left(x+\frac {y+z}2\right),$ 展开即是 $y^2+xy+yz-zx=0,$ 证毕.

这应该是最容易理解，步骤也是最少的，算算而已，不过，肯定无法能让题主及各位往来者心动~

---

下面求证 $\frac {PM}{MK}=\frac{PN}{NK},$这比例式决定了纯几何味道更纯，爽口，(此时字母如图2，用图2的字母. )


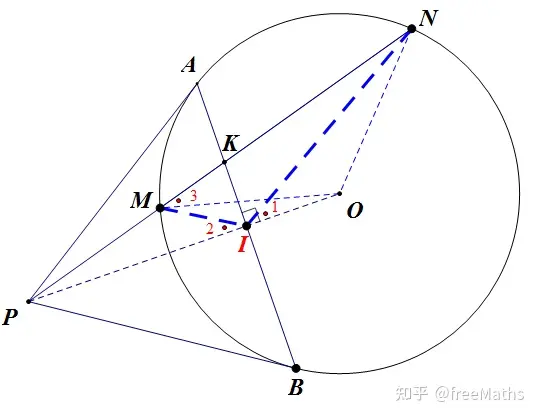
图 2 过点 P 引圆的两切线 A, B 分别为切点

记下 $PO\perp AB$ 于 $I$ 然后就忘掉 图1 的辅助线吧.



如图2，由 $PI\cdot PO=PB^2=PM\cdot PN,$ 知 $\color{red}{O,N,M,I}$ 四点共圆，于是 $\angle 1=\angle 3=\angle ONM=\angle 2,$ (注意ON=OM， $\angle 2$ 是四边形 ONMI 的外角).

又 $AI\perp PO,$ 所以 $IK$ 是 $\triangle INM$ 的内角平分线， $IP$ 是其外角平分线，从而

\[\frac {NK}{KM}=\frac {IN}{IM}=\frac {NP}{PM}\Rightarrow \frac {PM}{KM}=\frac {PN}{NK},\]

又证毕.

---

割线情况，8# forum.php?mod=viewthread&tid=7306

hejoseph

isee 发表于 2014-1-14 16:02
如图，$PB_1C_1,PB_2C_2$均为圆$O$割线，$B_1C_2,B_2C_1$相交于$A$。

求证：$\dfrac {PB}{PC}=\dfra ...

其实点 $A$、$Q$ 都在直线 $MN$ 上，这也是已知圆锥曲线及其外部一点，作过给定点圆锥曲线的切线的一个作图方法。

kuing

kuing 发表于 2014-6-2 18:03
bbs.pep.com.cn/thread-342328-31-1.html
601~603#

点评
@力工  看不见了，链接无效了。

还好以前截图存了档：
（就是图有点小，点击放大，也可 shift+鼠标滚轮放大，勉强能看清）