|
|
kuing
Posted at 2014-4-2 14:52:15
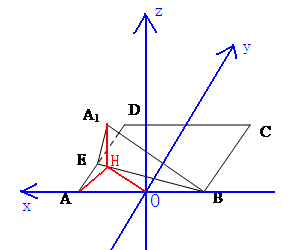
如图所示建立空间直角坐标系，其中原点 $O$ 为 $AB$ 中点。
不妨设 $AB=2$，记 $\angle ABE=\theta$，则 $\theta \in(0,c]$，其中 $c$ 为正常数（由 $AD$ 的长确定，这里不必具体给出），作 $A_1H\perp BE$ 于 $H$，则 $AH\perp BH$，故 $OH=1$ 且 $\angle AOH=2\theta $，于是 $H(\cos2\theta,\sin2\theta,0)$，又 $A_1H=AH=AB\sin\theta =2\sin\theta $，故此 $A_1(\cos2\theta,\sin2\theta,2\sin\theta)$。
假设 $A_1$ 恒在一个平面上，那么存在不全为 $0$ 的常数 $A$, $B$, $C$, $D$ 使得 $A\cos2\theta+B\sin2\theta+2C\sin\theta+D=0$ 对 $\theta \in(0,c]$ 恒成立。
令 $t=\tan(\theta/2)$，由万能公式代入得
\begin{align*}
A\cos2\theta+B\sin2\theta+2C\sin\theta+D=0
&\iff A\left(1-2\left(\frac{2t}{1+t^2}\right)^2\right) +2B\frac{2t}{1+t^2}\frac{1-t^2}{1+t^2} +2C\frac{2t}{1+t^2}+D=0\\
&\iff (A+D)t^4+4(C-B)t^3+2(D-3A)t^2+4(B+C)t+A+D=0,
\end{align*}
要上式对一定区间的 $t$ 恒成立，只能是 $A+D=C-B=D-3A=B+C=0$，解得 $A=B=C=D=0$，矛盾，从而 $A_1$ 不恒在一个平面上，所以选 D。 |
|
爪机专用
Posted at 2014-4-2 11:31:49
