|
|
 乌贼
乌贼
posted 2016-6-11 21:51
14题
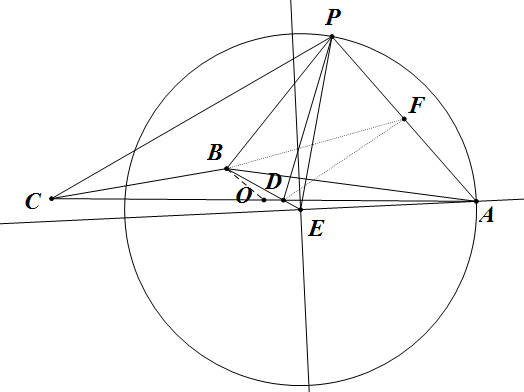
在平面$ABC$作$AE\perp CD$于$E$,过$AE$作一平面切以$B$为球心,$BA$为半径的球得球切园,$F,O$分别为$AP,AC$的中点。
\[AP\perp FD,AP\perp FB\riff AP\perp BE\]有点$P$在园上。$PQ$为$\triangle PAE$的高即为四面体$P-BCD$的高。当$D$点在$O$的左边时:设$OD=x\riff AP=AD=\sqrt3-x,AE=\dfrac{\sqrt3-x}{\sqrt{x^2+1}}$
\[PQ=\dfrac12(\sqrt3-x)(\sqrt3+x)\riff V_{P-BCD}\le\dfrac{\sqrt3}4\](当$x=0$时取得)
当$D$点在$O$的右边时:$TM$的运算……
不如代数设点$P(x_0,y_0,z_0)$,联立$AP=AD,PB=2$及$PA\perp BD$求得\[x_0=f(CD)\]来得快……不懂空间垂线斜率
|
|