平凡但较难证明的几何题：中点+等线段

isee

题目：如图，Rt$\triangle ADE\sim$Rt$\triangle ABC$（两三角镜面相似），连接$CE$，取$CE$中点$F$．
求证：$FB = DF$且$\angle DFB = 2\angle ACB$．


好几年了，还好得到个“伪”复数证明。随后帖，玩下，先。

乌贼

\[ \triangle ADE\cong \triangle ADE_1\cong \triangle AD'E'\cong \triangle AD'E'_1\\\triangle ABC\cong \triangle ABC_1\cong \triangle AB'C'\cong \triangle AB'C'_1 \]
还有角：\[\begin{align*}
\angle DFB&=\angle DFE+\angle EFB=\angle E'CE+\angle ECC_1+\angle FBC\\&=\angle E'CA+\angle ACF+\angle ECC'+\angle EC'C\\&=\angle ACF+\angle ECC'+\angle EC'C+\angle ECE'\\&=2\angle ACB
\end{align*}  \]

kuing

俩三角形还是不要重叠比较好看，下面狠心地将它们分开一下，也就是画成下面这样子，结论应该一样。



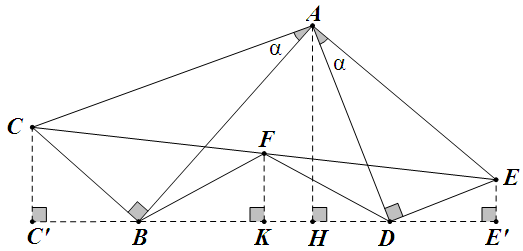
这样是熟悉的图形，你没记错，《撸题集》里有一样的图形（在哪页自己找喔），照套那里的法子，有
\[\frac{BC'}{AH}=\tan\alpha=\frac{DE'}{AH}
\riff BC'=DE',\]
由 $F$ 为中点有 $KC'=KE'$，所以 $KB=KD$，即 $FB=FD$。

由
\[\frac{CC'}{BH}=\tan\alpha=\frac{EE'}{DH},\]
得
\[FK=\frac12(CC'+EE')=\frac12(BH+DH)\tan\alpha=BK\tan\alpha,\]
可见 $\angle FBD=\angle FDB=\alpha$，从而 $\angle DFB = 2\angle ACB$。

kuing

回复 3# kuing

要是真按楼主的原图来作同样的辅助线，会成这个样子：



表示已经有点眼花，不过还是能分辨出来的，这时，楼上的证法前半不用变，而后半则改为
\[FK=\frac12(CC'-EE')=\frac12(BH-DH)\tan\alpha=BK\tan\alpha,\]
结论如无意外地相同了。

isee

\[ \triangle ADE\cong \triangle ADE_1\cong \triangle AD'E'\cong \triangle AD'E'_1\\\triangle ABC\co ...
乌贼 发表于 2017-6-14 21:40

这个证得极公平咯，大的小的均串一起。


其实麻烦了。

把只要有E'的都擦掉，同样的只有要C’都擦掉，剩余的图足够用了。

isee

俩三角形还是不要重叠比较好看，下面狠心地将它们分开一下，也就是画成下面这样子，结论应该一样。



这样 ...
kuing 发表于 2017-6-14 22:53

还是熟悉的“味道”。

==================
与图形的位置无关，结果均成立。

kuing

回复 5# isee

乌贼那图我一瞄就眼花，不敢看……

乌贼

回复楼上两位，我的证明往往是通过画图的过程画出来的，也不想擦掉了

乌贼

回复 5# isee
想简单明了

isee

回复 8# 乌贼


    这叫反思。。。。。。

乌贼

回复 10# isee
为得到图形，我得先画等腰梯形$B'BC'C$，然后……

色k

回复 9# 乌贼

这样就好看多了，而且仅看图都能知道怎么证了，可省去文字，nice proof !

乌贼

我说怎么那么眼熟，与链接6楼差不多，等边变等腰，连接$CE$，取中点再和$D,G$连接就是本题了
forum.php?mod=viewthread&tid=4595&extra=page=3

isee

在9楼的形中

图中两个阴影三角是全等的，可以将其中一个旋转而得到另一个。

用复数与向量表示就是（所以说是“伪”复数法）:

记$$\angle CAB=\angle EAD=\theta,$$则

$$2\vv {FB}=\vv {AC}\cdot\mathrm {e}^{2\theta\mathrm i}-\vv {AE}.$$

$$2\vv {FD}=\vv {AE}\cdot\mathrm e^{-2\theta\mathrm i}-\vv {AC}.$$

$$2\vv {FD}\cdot\mathrm e^{2\theta\mathrm i}=\vv {AE}-\vv {AC}\cdot\mathrm e^{2\theta\mathrm i}=-2\vv {FB}.$$

isee

向量另证，受kuing在特殊情况中下的提示，证“垂直平分”。整理 by iC。

记$$\frac {DE}{AD}=
\frac{CB}{AB}=k.$$
连接$DB$，并取其中点$G$，连接$FG$，则在四边形$DBCE$中（如果不习惯主楼图，请看3楼图）$$2\vv {GF}=\vv{BC}+\vv{DE}=k\cdot \vv{BA}\cdot \mathrm i+k\cdot \vv{AD}\cdot \mathrm i=k(\vv{BA}+\vv{AD})\cdot \mathrm i=2k\vv{DG}\cdot \mathrm i=2k\vv{GB}\cdot \mathrm i.$$
这表明$$FG \perp DB,\triangle DGF\sim \triangle ABC.$$
于是结论得证.

这是“真向量”证明，终于了结了，我多年的“心事”。

kuing

回复 15# isee

我对几何还是不及你敏锐，昨天证了那题，完全想不起这题……

PS、擅自给“特殊情况”加了昨天那题的链接及修改了一处笔误