逛空间看到的合肥二模12题，角相等与边等比、面积等比

kuing

已知点 $I$ 在 $\triangle A B C$ 内部，$A I$ 平分 $\angle B A C, \angle I B C=\angle A C I=\frac{1}{2} \angle B A C$．对满足上述条件的所有 $\triangle A B C$，下列说法正确的是

• $\triangle A B C$ 的边长一定成等差数列；
• $\triangle A B C$ 的三边长一定成等比数列；
• $\triangle A B I, \triangle A C I, \triangle C B I$ 的面积一定成等差数列；
• $\triangle A B I, \triangle A C I, \triangle C B I$ 的面积一定成等比数列．

依题意，如图所示，因 $IA=IC$，故
\[\frac{IB}{IA}=\frac{IB}{IC}
\iff\frac{\sin x}{\sin y}=\frac{\sin z}{\sin x}
\iff\sin^2x=\sin y\sin z,\]
积化和差并注意 $4x+y+z=\pi$，有
\[\sin^2x=\frac{\cos(y-z)-\cos(y+z)}2
=\frac{\cos(y-z)+\cos4x}2,\]
所以
\[\cos(y-z)=2\sin^2x-\cos4x,\]
那么
\begin{align*}
\sin(x+y)\sin(x+z)&=\frac{\cos(y-z)-\cos(2x+y+z)}2\\
&=\frac{2\sin^2x-\cos4x+\cos2x}2\\
&=\sin^22x,
\end{align*}
根据正弦定理，此即 $bc=a^2$，即三边等比。

乌贼

作$ ABI $外接圆交$ AC $于$ D $，有\[ \triangle ABI\cong \triangle CDI \]即\[ AB=CD \]又\[ \angle CAI=\angle IBC \]所以$ CB $为园的切线，故\[ CB^2=CD\times AC=AC\times AB \]

kuing

回复 2# 乌贼


这个证法才正宗

isee

回复 2# 乌贼


我在想三角形ABC的外接圆，一堆相似弄晕了，结果你已经有了，不想了。
===

因为这辅助线实在是太简了

isee

回复  乌贼


这个证法才正宗
kuing 发表于 2018-3-24 20:32

主要是有结论了。。。求比证难。。。

kuing

回复 5# isee

其实我发现 D 几乎是对的，只需改变一下次序，或者换个表达方式，它就会是对的

kuing

续楼上：

下面证明 $\S{CAI}$, $\S{ABI}$, $\S{BCI}$ 成等比数列。

依然玩三角变换，依然用1楼的图以及得到的 $\sin^2x=\sin y\sin z$，我们有
\begin{align*}
\frac{\S{CAI}}{\S{ABI}}&=\frac bc=\frac{\sin(x+y)}{\sin(x+z)},\\
\frac{\S{ABI}}{\S{BCI}}&=\frac{c\sin y}{a\sin x}
=\frac{\sin(x+z)\sin y}{\sin2x\sin x}
=\frac{\sin(x+z)\sin y}{2\sin^2x\cos x}
=\frac{\sin(x+z)}{2\sin z\cos x},
\end{align*}
因此只需证明
\[2\sin z\cos x\sin(x+y)=\sin^2(x+z),\]
依然利用积化和差及 $4x+y+z=\pi$，有
\begin{align*}
\LHS&=\bigl( \cos(x+y-z)-\cos(x+y+z) \bigr)\cos x\\
&=\frac{\cos(2x+y-z)+\cos(y-z)-\cos(y+z)-\cos(2x+y+z)}2\\
&=\frac{-\cos(2x+2z)+2\sin y\sin z+\cos2x}2\\
&=\frac{-\cos(2x+2z)+2\sin^2x+\cos2x}2\\
&=\frac{1-\cos(2x+2z)}2\\
&=\RHS,
\end{align*}
即得证。

证是证了出来，但感觉肯定绕了弯路……俺不行了，你们来……

kuing

@乌贼 @isee  坐等面积等比的平几证法

isee

@乌贼 @isee  坐等面积等比的平几证法
kuing 发表于 2018-3-25 11:17

布洛卡点 是逃脱不了干系的……

isee

一般结论，只需要$\angle IAB=\angle IBC=\angle ICA$，即点$I$三角形$ABC$的布洛卡点，则(与此题有关的）
$$IA=\frac{b^2c}{\sqrt{a^2b^2+b^2c^2+c^2a^2}},IB=\frac{c^2a}{\sqrt{a^2b^2+b^2c^2+c^2a^2}},IC=\frac{a^2b}{\sqrt{a^2b^2+b^2c^2+c^2a^2}},$$
$$IA:IB:IC=b^2c:c^2a:a^2b,$$
$$S_{\triangle IAB}:S_{\triangle IBC}:S_{\triangle ICA}=b^2c^2:c^2a^2:a^2b^2.$$

kuing

回复 10# isee

原来有这样的结论，既然如此，那我就继续将1楼的三角玩法进行到底！

图就懒得重画了，直接拿1楼的图改一个字母：



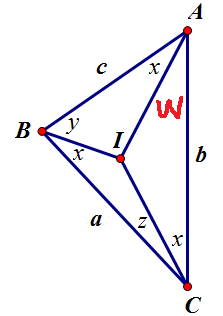
因为
\[1=\frac{IA}{IB}\cdot\frac{IB}{IC}\cdot\frac{IC}{IA}
=\frac{\sin y}{\sin x}\cdot\frac{\sin z}{\sin x}\cdot\frac{\sin w}{\sin x},\]
积化和差并注意 $3x+y+z+w=\pi$，有
\begin{align*}
\frac{2\sin^3x}{\sin y}&=2\sin z\sin w\\
&=\cos(z-w)-\cos(z+w)\\
&=\cos(z-w)+\cos(3x+y),
\end{align*}
所以
\[\cos(z-w)=\frac{2\sin^3x}{\sin y}-\cos(3x+y),\]
那么
\begin{align*}
\sin(x+z)\sin(x+w)&=\frac{\cos(z-w)-\cos(2x+z+w)}2\\
&=\frac{\frac{2\sin^3x}{\sin y}-\cos(3x+y)+\cos(x+y)}2\\
&=\frac{\sin^3x}{\sin y}+\sin x\sin(2x+y)\\
&=\frac{\sin x}{\sin y}\bigl(\sin^2x+\sin y\sin(2x+y)\bigr)\\
&=\frac{\sin x}{\sin y}\left( \sin^2x+\frac{\cos2x-\cos(2x+2y)}2 \right)\\
&=\frac{\sin x}{\sin y}\cdot\frac{1-\cos(2x+2y)}2\\
&=\frac{\sin x}{\sin y}\cdot\sin^2(x+y),
\end{align*}
所以有
\[\frac{\sin y}{\sin x}=\frac{\sin^2(x+y)}{\sin(x+z)\sin(x+w)}
\iff\frac{IA}{IB}=\frac{b^2}{ca},\]
另外两式同理，即有
\[\frac{IA}{IB}=\frac{b^2}{ca},
\frac{IB}{IC}=\frac{c^2}{ab},
\frac{IC}{IA}=\frac{a^2}{bc},\]
所以
\[IA:IB:IC=b^2c:c^2a:a^2b.\]

至于 $IA$ 等的具体表达式明天再玩，现在先玩面积的，这回就不走7楼的路了，因为7楼明显是弯路。

根据上述结论，有
\[\frac{\S{IAB}}{\S{IBC}}=\frac{IA\sin(\pi-x-y)}{IC\sin(\pi-x-z)}
=\frac{IA}{IC}\cdot\frac{\sin(x+y)}{\sin(x+z)}
=\frac{bc}{a^2}\cdot\frac bc=\frac{b^2}{a^2},\]
另外两式同理，即有
\[\frac{\S{IAB}}{\S{IBC}}=\frac{b^2}{a^2},
\frac{\S{IBC}}{\S{ICA}}=\frac{c^2}{b^2},
\frac{\S{ICA}}{\S{IAB}}=\frac{a^2}{c^2},\]
所以
\[\S{IAB}:\S{IBC}:\S{ICA}=b^2c^2:c^2a^2:a^2b^2.\]

其妙

没审核是不是这道题（某网友解答）：

kuing

回复 12# 其妙

审核一下又不用几分钟。
是这题，而且证得很漂亮。

kuing

这样一来，我那些三角法就完全可以扔掉了，都是弯路。

一般情形，仿12#，有
\[\frac{IB}c=\frac{\sin x}{\sin\angle AIB}=\frac{\sin x}{\sin(\pi-x-y)}=\frac{\sin x}{\sin B},\]
同理
\[\frac{IC}a=\frac{\sin x}{\sin C},\frac{IA}b=\frac{\sin x}{\sin A},\]
所以
\[IA:IB:IC=\frac b{\sin A}:\frac c{\sin B}:\frac a{\sin C}=\frac ba:\frac cb:\frac ac=b^2c:c^2a:a^2b.\]

至于面积比，11#的应该没弯吧……

敬畏数学

回复 12# 其妙
又是一个妙解！

游客

"2011年北京大学保送生平面几何试题（布洛卡点）的六种证法"

搜这个，居然把北大试题当一般试题考了。。。

guanmo1

回复 16# 游客
三边成等比（差）数列三角形的勃罗卡点（角）的性质已有系统研究。现在关于勃罗卡点的研究的一个最新方向是一般多边形存在勃罗卡点的充要条件。