一道会考函数

hjfmhh

facebooker

a=2/3  b=4/3 取得最小值8/3

走走看看

回复 2# facebooker

怎么解析呢？
根据题意易得 | a+|x-b| |≥  | |x|-2|x-1| |，如何来解呢？

realnumber

回复 3# 走走看看


    左右分别画函数图象？

facebooker

回复 3# 走走看看

不会啊 如果会做 我早写了。。。

kuing

回复 4# realnumber

嗯，图形并不难画，无非就是下面两种情况：
`a\geqslant0` 的 V 型：

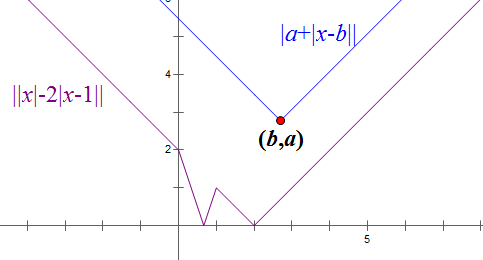
`a<0` 的 W 型：

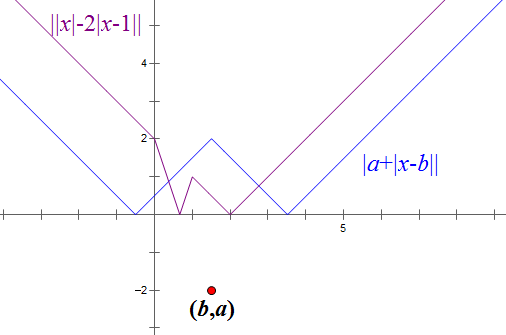
明显后者是不可能恒成立的，所以只有前者，这样就能看出肯定有 a+b>=2，那么再用柯西 (1/2+1)(2a^2+b^2)>=... 就知道结果了。

当然，以上的看图说话只是分析时用，实际写装逼解答时当然不能提这些，而是去凑不等式。

这题的凑比以往的还简单，我们的目标是要凑出 a+b>=2，而这只要目测就能发现代入 x=0 立马就有了！于是解答过程如下。

解：因为当 `x=0` 时成立，所以 $\bigl|a+\abs b\bigr|\geqslant2$，于是
\[
4\leqslant(a+\abs b)^2
\leqslant\left(\frac12+1\right)(2a^2+b^2),
\]即得 `2a^2+b^2\geqslant8/3`。

最后，当然还需要验证取等，也就是证明如下不等式的确是恒成立的
\[
\frac23+\left|x-\frac43\right|\geqslant\bigl|\abs x-2\abs{x-1}\bigr|,
\]通过分类讨论总能证出来，我就懒得写了……

反正基本套路还是那样——通过图形先猜出结果，再凑不等式，最近我都扯过几次了，像：
forum.php?mod=viewthread&tid=6246
forum.php?mod=viewthread&tid=6127

敬畏数学

回复 6# kuing
两种方法。牛。