|
|
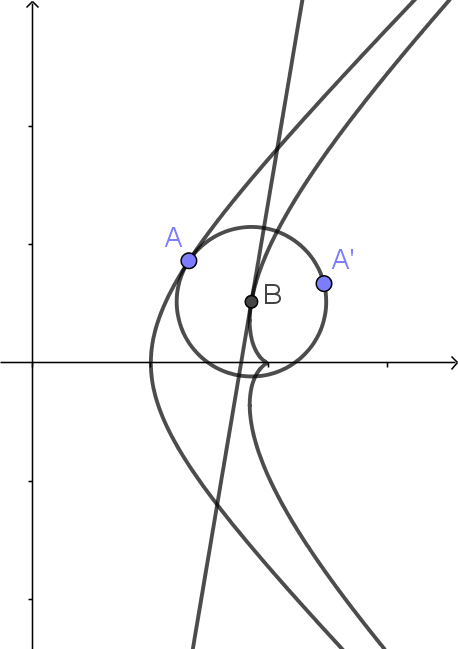
Last edited by hbghlyj 2023-2-23 22:16双曲线$x^2-y^2=1$上一点$A$,曲率中心$B$的轨迹是$$-64 + 48 x^2 - 12 x^4 + x^6 - 48 y^2 + 12 x^2 y^2 + x^4 y^2 - 12 y^4 -
x^2 y^4 - y^6=0$$作$B$处的切线,$A$关于它的对称点$A'$的轨迹是\begin{gathered}-65536+147456 x^2-123392 x^4+52416 x^6-12545 x^8+1725 x^{10}-128 x^{12}+4 x^{14}-147456 y^2+195584 x^2 y^2\\-72000 x^4 y^2+7276 x^6 y^2+1287 x^8 y^2-336 x^{10} y^2+20 x^{12} y^2-123392 y^4+72000 x^2 y^4-7014 x^4 y^4-438 x^6 y^4\\-192
x^8 y^4+36 x^{10} y^4-52416 y^6+7276 x^2 y^6+438 x^4 y^6+32 x^6 y^6+20 x^8 y^6-12545 y^8-1287 x^2 y^8\\-192 x^4
y^8-20 x^6 y^8-1725 y^{10}-336 x^2 y^{10}-36 x^4 y^{10}-128 y^{12}-20 x^2 y^{12}-4 y^{14}=0\end{gathered}

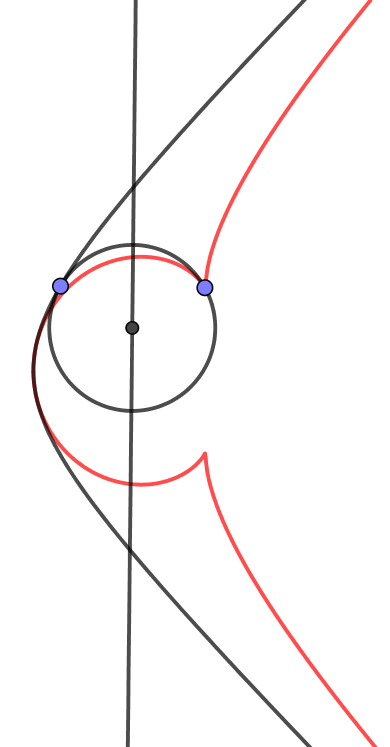
近似地,当$B$处的切线为竖直的时,$A'$的轨迹出现一个尖点(cusp),这时,$A\left(\frac12\sqrt{3\over2},\frac1{\sqrt2}\right),B\left(\frac32\sqrt{3\over2}, \frac1{2\sqrt2}\right),A'\left(2\sqrt{3\over2},\frac1{\sqrt2}\right)$

|
|