|
|
Last edited by hbghlyj 2023-6-11 17:25When can't a real definite integral be evaluated using contour integration?
一些较旧的复分析书指出 $ \displaystyle \int_{0}^{\infty}e^{-x^{2}} \ dx$ 无法使用围道积分进行计算。
上述主张的一个著名例子是 Watson,Complex Integration and Cauchy's theorem (1914),第 79 页:
![Xx2xl[1].png Xx2xl[1].png](data/attachment/forum/202211/27/204835w2pi6v56l6izvrvy.png)
但现在知道这不是真的。
例如 H. A. Priestley - Introduction to Complex Analysis 第二版 (2003) 第250页
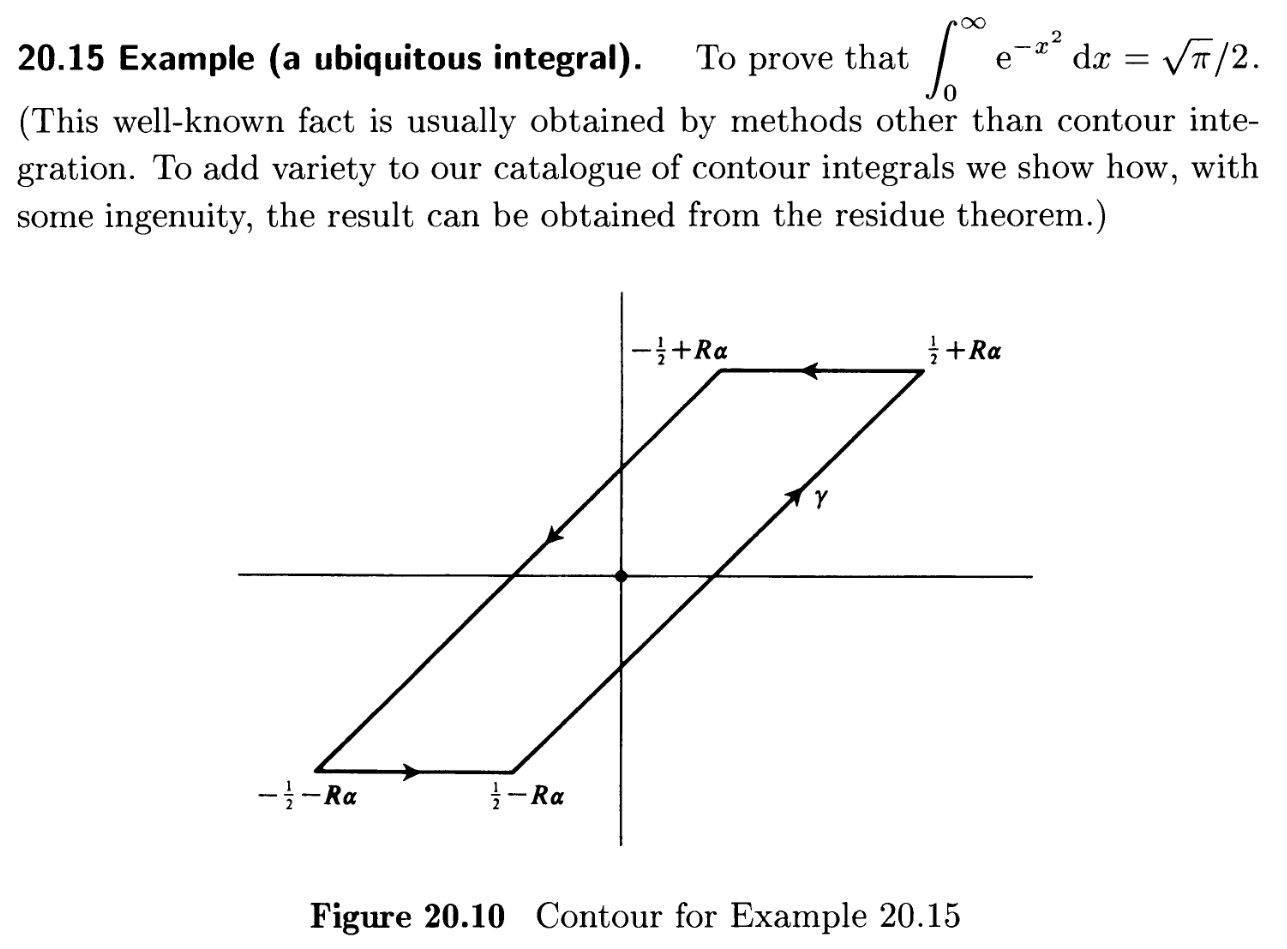
Solution Let $\alpha=\mathrm{e}^{\mathrm{i} \pi / 4}$. We integrate $f(z)=\mathrm{e}^{\mathrm{i} \pi z^2} \operatorname{cosec} \pi z$ round the contour $\gamma$ in Fig. 20.10 and obtain
\[
\int_\gamma f(z) \mathrm{d} z=2 \pi \text { i res}\{f(z) ; 0\}=2 \mathrm{i} .
\]
On the slanting sides, we have $z=t \alpha \pm \frac{1}{2}(-R \leqslant t \leqslant R)$ and $f(z)=\pm(\sec \pi t \alpha) \mathrm{e}^{\mathrm{i} \pi\left(t^2 \pm t \alpha+\frac{1}{4}\right)}$, so that their combined contribution to $\int_\gamma f(z) \mathrm{d} z$ is
\[
\begin{aligned}
&\int_{-R}^R \alpha\left(\mathrm{e}^{\mathrm{i} \pi\left(t^2+t \alpha+\frac{1}{4}\right)}+\mathrm{e}^{\mathrm{i} \pi\left(t^2-t \alpha+\frac{1}{4}\right)}\right) \sec \pi t \alpha \mathrm{~d} t \\
&=2 \mathrm{i} \int_{-R}^R \mathrm{e}^{-t^2} \mathrm{~d} t=\frac{4 \mathrm{i}}{\sqrt{\pi}} \int_0^{R \sqrt{\pi}} \mathrm{e}^{-x^2} \mathrm{~d} x .
\end{aligned}
\]
On the horizontal sides, $z=\pm R \alpha+t(-1 / 2 \leqslant t \leqslant 1 / 2)$ and an estimate of their contribution to the integral is given by
\[
\left|\int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{\mathrm{e}^{\mathrm{i} \pi\left(\mathrm{i} \alpha^2 \pm 2 R \alpha t+t^2\right)}}{\sin \pi(\pm R \alpha+t)} \mathrm{d} t\right| \leqslant \int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{2 \mathrm{e}^{-\pi R^2+R \pi t \sqrt{2}}}{\mathrm{e}^{\pi R / \sqrt{2}}-\mathrm{e}^{-\pi R / \sqrt{2}}} \mathrm{~d} t .
\]
Taking the limit as $R \rightarrow \infty$, the required result is obtained. |
|