证明Pascal定理

hbghlyj

杨圣汇 Quick Symbolic Proof of Pascal Line

辅助函数—找到两线的交点:

1. segmentIntersection[p1_List, p2_List, p3_List, p4_List] :=
2. Block[{u, v}, Module[{sol},
3.    sol = Solve[u*(p2 - p1) + p1 == v*(p4 - p3) + p3, {u, v}];
4.    {u, v, u*(p2 - p1) + p1} /. sol[[1]]]]

Copy the Code

定义椭圆（或双曲线）上点的函数

1. pt[t_] := {m*Cos[t], n*Sin[t]}
2. pt2[t_] = {m*Sec[t], n*Tan[t]}

Copy the Code

定义交点$g,h,k$ g = segmentIntersection[pt[a], pt[f], pt[c], pt[d]][[3]]; h = segmentIntersection[pt[a], pt[b], pt[d], pt[e]][[3]]; k = segmentIntersection[pt[b], pt[c], pt[e], pt[f]][[3]]; Copy the Code

通过Cross检查GHK是否共线。想法是 GHK 共线当且仅当 GH 的法向量 V 垂直于 HK ( V⋅HK=0 )

1. Cross[g - h].(h - k) // Simplify

Copy the Code

上面的代码在不到 1 秒的时间内返回 0。因此它完成了证明。对于双曲线需要用 pt2[t]，结果是相同的。

TSC999

非常棒的方法。难怪大家对复平面解析方法不感兴趣，原来是天外有天啊。

已知平面上的四点 A、B、C、D 的复坐标为 a, b, c, d,  如何用这种方法求出 AB 与 CD 的交点坐标？

uk702

gitee.com/cgps/Analytic-Geometry-Mathematica 提供了一个用mathematica写的解析几何求解器，可以学习一下。

个人认为大多时候复数的几何方法能用的手段更多。

hbghlyj

TSC999 发表于 2023-4-5 05:08
如何用这种方法求出 AB 与 CD 的交点坐标？

Geogebra 也通过叉积计算来计算2线的交点。

hbghlyj 发表于 2022-1-6 10:15
原来GeoGebra使用的是齐次坐标
二维点的坐标计算方法是$\left(\frac xz,\frac yz\right)$
自由点的z坐标是1 ...

Calculating where projective lines intersect
Finite example
Consider the lines

y = 3x + 2

and

y = x + 4

The lines intersect at the point where x = 1 and y = 5 in the ordinary plane. If we embed each line in the projective plane and take the intersection there, we get the embedding of the point (1, 5) in the projective plane. Recall that we associate the point (x, y) in the ordinary plane with (x, y, 1) in the projective plane.

We have the cross product

((3, -1, 2)) × ((1, -2, 4)) = ((-2, -10, -2))

which is associated with the point (-2, -10, 2), which is in the same equivalence class as (1, 5, 1), which is the embedding of the point (1, 5) in the projective plane.

hbghlyj

Jürgen Richter-Gebert (auth.) - Perspectives on Projective Geometry_ A Guided Tour Through Real and Complex Geometry-Springer-Verlag Berlin Heidelberg (2011)

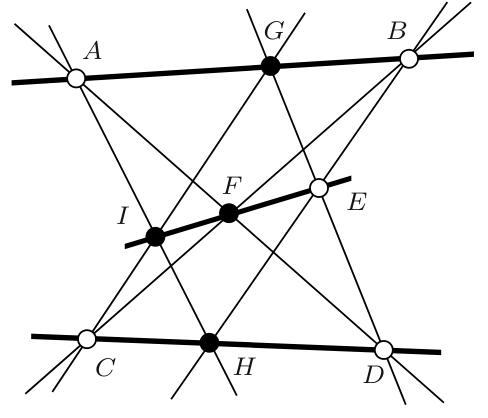
我们将给出 Pappos 图的一系列几何构造。 我们从五个自由点 A、B、C、D、E 开始。画一些直线并画出交叉点。 构造中其余四个交点的坐标可以通过叉积计算 F = (A × D) × (B × C), G = (A × B) × (D × E), H = (C × D) × (B × E), I = (A × H) × (C × G). 最终的共线性归结为 $\det(E, F, I) = 0$.

1. a={a1,a2,a3};
2. b={b1,b2,b3};
3. c={c1,c2,c3};
4. d={d1,d2,d3};
5. e={e1,e2,e3};
6. f=Cross[Cross[a,d],Cross[b,c]];
7. g=Cross[Cross[a,b],Cross[d,e]];
8. h=Cross[Cross[c,d],Cross[b,e]];
9. i=Cross[Cross[a,h],Cross[c,g]];
10. Det[{e,f,i}]//Simplify

Copy the Code

输出0
它表明，当我们执行一系列构造时，无论初始条件 A、B、C、D、E 的坐标是什么，最终的行列式都将为零。这可能有两个原因。
或者是在构造过程中，我们遇到了一种退化情况（例如两条相同的线相交），引入了一个零向量作为中间结果。
或者所有操作都是非退化的并且最后的点 E、F、I 是共线的。

hbghlyj

uk702 发表于 2023-4-8 23:35
个人认为大多时候复数的几何方法能用的手段更多。

这取决于问题。对于这个特定问题，它是纯射影性质。

uk702

另外，MMA 12 版本内置的几何功能也很（极其）强大。ref/GeometricSceneref/FindGeometricConjectures

角	平分线	三角形的中心	九点圆
欧几里德的《元素》	勾股定理	维维亚尼定理	完美三角形剖析
求未知角	求未知半径	求未知边长	求正方形的面积
发现简单的猜想：泰勒斯定理	以多种方式形成定理：帕普斯六边形定理	过滤猜想：拿破仑定理	改进定理陈述：Finsler-Hadwiger 定理

内容来自下面网页：https://www.wolfram.com/language ... zh?product=language