通过6点圆盘排线法快速应用帕斯卡定理

lxz2336831534

已知圆锥曲线上6点，标号为123456，由帕斯卡定理可知，三个对边交点共线，那么形成的帕斯卡线有哪些情况呢
如下图，作一个6个格子的圆盘随机填入6个数，如

然后在每一个数旁边写入其前一个格子中的数，如

则三组相对的格子中直线交点共线，如61和25的交点，13和42的交点，35和64的交点共线。圆盘中每个数只可出现两次，且相对的格子中4个数都不同。
当圆曲上6点退化为5点时，重合的点标号相同，如

由于6个点减少为5个点，则6个标号可以减少为5个顺序标号，如

11则为1点的切线。

• 证明6点圆盘排线法的正确性。
• 分别计算当圆曲上点数为4,5,6,7时的帕斯卡线条数。
• 圆盘相对格子中的两条直线交换标号后所得的两条新直线的极点和原先两条直线的交点共线，如
  14,23两直线的极点或12,34两直线的极点和13,42的交点共线。该性质由完全四点形性质易证。

lxz2336831534

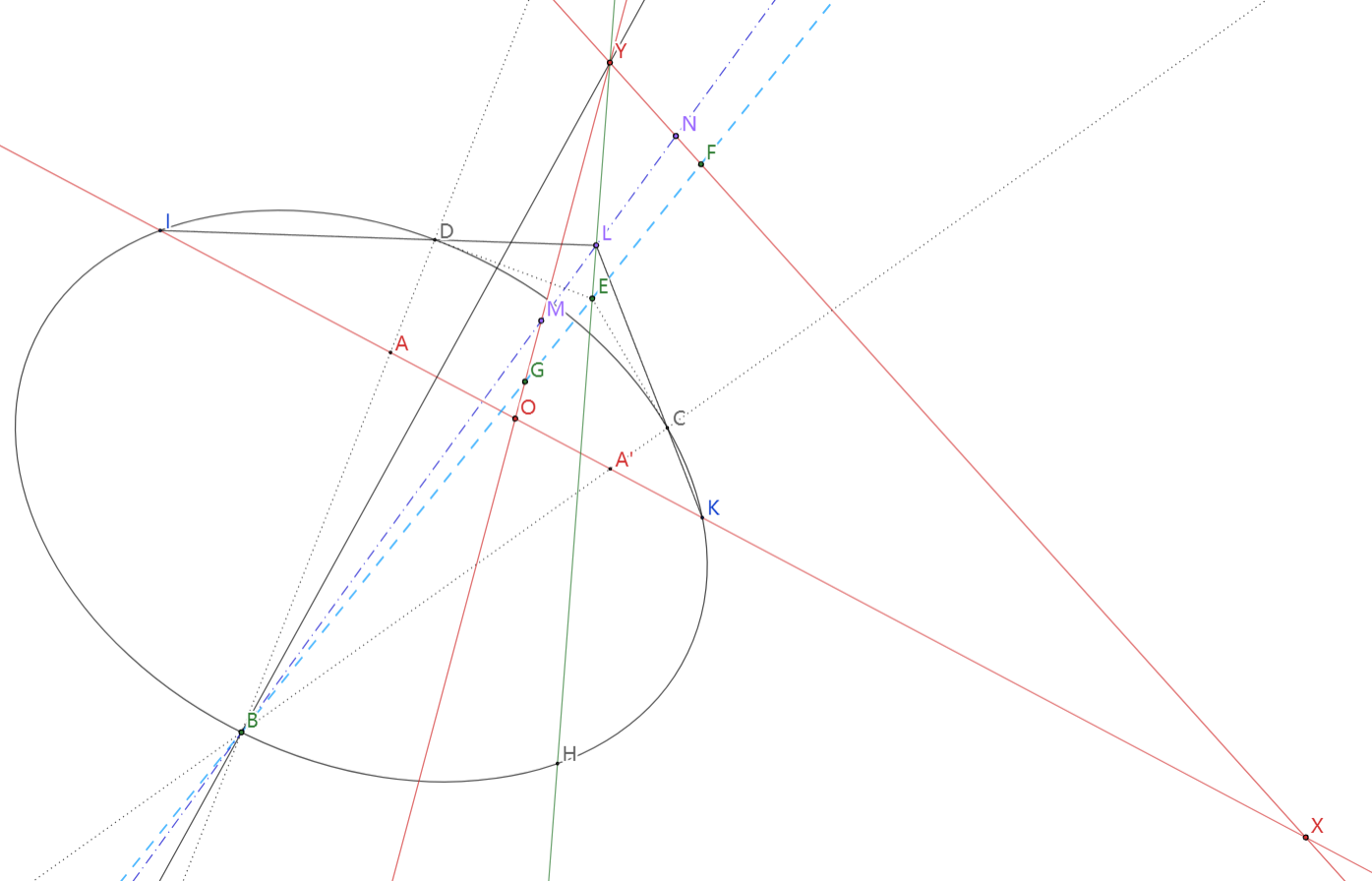
今给定一椭圆上有三点B, C, D,作自极三点形 OXY, D, C二点的切线交于点E,BE分别交OY, XY于G, F二点,OX分别交BD, BC于A, A′二点.若有(AA'OX) =-1,
①问(BEGF)=?
②若ID和KC交于L点，BL分别交OY和YX于M,N二点，证明B，L调和分割M，N.

第一问已证forum.php?mod=viewthread&tid=13705
应用帕斯卡定理和六点圆盘排线法速证第二问

对D,C,K,B,I 5点应用帕斯卡定理可知BI,DC的交点；ID,KC的交点L；BK和D的切线交点三点共线。
对对边ID,KC应用上述性质3可知L和DC的极点E，IK的极点Y三点共线
所以(B,L,M,N) ⌆ Y(B,E,G,F) ⌆ (B,E,G,F)
又由第一问(BEGF)=-1所以(BLMN)=-1，证毕

hbghlyj

lxz2336831534 发表于 2025-4-14 14:51
点数为4,5,6,7时的帕斯卡线条数

点数为6时的帕斯卡线条数$=5!/2=60$