|
|
Last edited by hbghlyj 2023-8-27 06:08Functional Analysis I 2017: Problem Sheet 1 Hilary Ann Priestley
第6题是有关Sequence space的
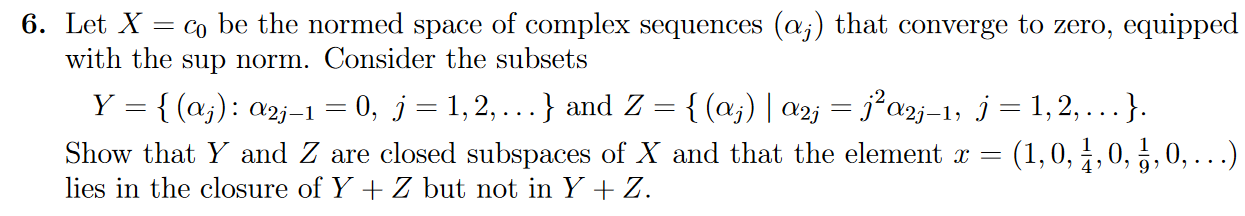
我有一点想法:
设$e_1=(1,0,0,\dots),e_2=(0,1,0,\dots),\dots$
则$x=\sum_{j=1}^\infty\frac1{j^2}e_{2j-1}$
证明$\boldsymbol{x\notin Y+Z}$:设$x=y+z,y\in Y,z\in Z$,则$z_{2j-1}=x_{2j-1}-y_{2j-1}=\frac1{j^2}$,则$z_{2j}=1$与$z_j\to0$矛盾.
证明$\boldsymbol{x\in\overline{Y+Z}}$:对于$y=\frac1{j^2}e_{2j-1}+e_{2j}\in Y,z=-e_{2j}\in Z$有$e_{2j}=y+z$
然后不会做了 不理解closure of Y+Z怎么用 不理解closure of Y+Z怎么用 |
|