$\{x∈ℓ^2:(j x_j)∈ℓ^1\}$

hbghlyj

Functional Analysis I 2017: Problem Sheet 2 Hilary Ann Priestley

$$X:=\left\{x∈ℓ^2:\left(j x_j\right)∈ℓ^1\right\} ⊂ ℓ^2$$Is $X$ a Banach space?

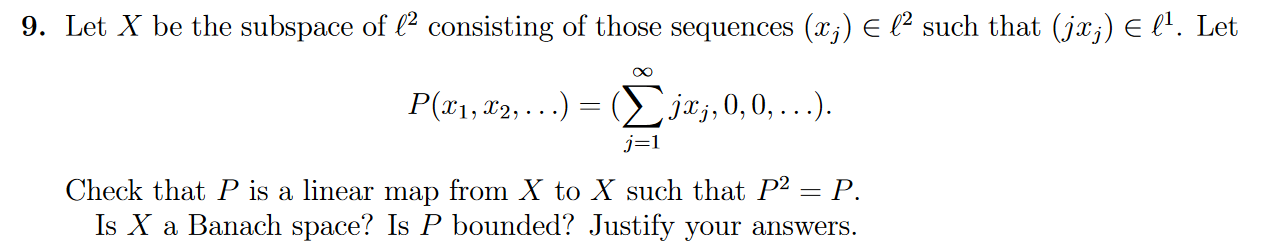
我猜答案是Yes, $X$ is a Banach space.
因$X\subset ℓ^2$且$ℓ^2$ is a Banach space，为证明$X$ is a Banach space只需证明$X$ is closed in $ℓ^2$,即

$x^{(n)}∈X$依$\ell^2$范数收敛于$x∈\ell^2$，证明$x∈X$.

因$x∈X$等价于$∑_jj|x_j|<∞$，问题可以转化为：

$x^{(n)}$依$\ell^2$范数收敛于$x$，且$\forall n$有$∑_jj|x^{(n)}_j|<∞$，证明$∑_jj|x_j|<∞$.

又转化为问题：
$\begin{rcases}∑_j(x_j-x^{(n)}_j)^2\to0\\
∑_jj|x_j^{(n)}|<\infty\\
∑_jx_j^2<\infty
\end{rcases}$是否能推出$∑_jj|x_j|<∞$

hbghlyj

剛才我猜错，现在觉得$X$不是Banach space.
取$x_n=(1,\frac12,\dots,\frac1n,0,\dots),x=(1,\frac12,\dots)$
则$x_n\to x$
$x_n\in X$且$x\notin X$.

---

第2问Is $P$ bounded?
很简单：
Let $e_1=(1,0,…),e_2=(0,1,0,…),…$ then $Pe_n=ne_1$, so $P$ is unbounded.

Czhang271828

$X$ 包含所有有限数列, 而有限数列在 $\ell^2$ 中稠密. 从而 $X$ 是 Banach 空间当且仅当 $X=\ell^2$. 而 $\ell^2$ 显然比 $X$ 来得大, 考虑 $(1/n)_{n\geq 1}\in\ell^2$ 即可.

方法类似 forum.php?mod=redirect&goto=findpost& … =11384&pid=55900