圆锥曲线中动圆过定点问题

1+1=？

今天看见群友的一个问题，看着是熟悉的动圆定点问题，就做了一下，然而还是发现了一些新奇。
已知点 $F_1(-2,0), F_2(2,0), M$ 是圆 $O: x^2+y^2=2$ 上任意一点，点 $F_1$ 关于点 $M$ 的对称点为 $N$，线段 $F_1 N$ 能中垂线与直线 $F_2 N$ 相交于点 $T$，记点 $T$ 的轨迹为曲线 $C$．
（1）求曲线 $C$ 的方程：
（2）过直线 $x=1$ 上一点 $P$ 作曲线 $C$ 的两条切线，交直线 $y=x$ 于 $A, B$ 两点，证明：以 $A B$为直径的圆恒过定点．
我以射影几何角度做了一下 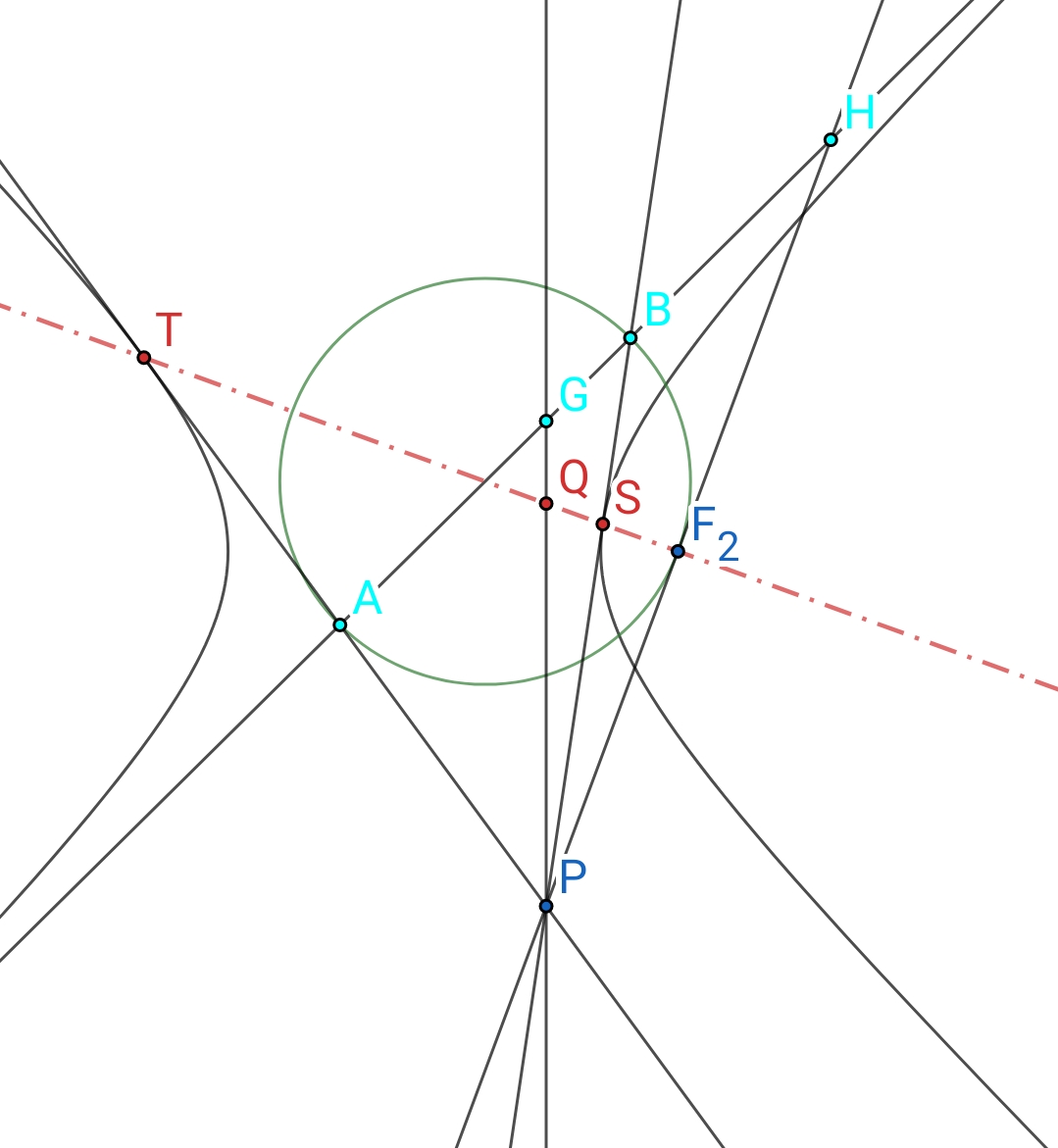引理1：$\Gamma$为非退化二次曲线。
$P$ 为 $\Gamma$ 上一定点，且 $Q$ 为定点
$A,B$为$\Gamma$上动点。可知此时 $P A$ 到 $P B$ 的变换为对合变换。

对该情形配极：$R$ 为 $\Gamma$ 上定点，$l$ 为定直线，$S$ 是 $l$ 上一点。$P, Q$ 为$\Gamma$上动点 $P, Q, R$ 的切线分别是 $A S, B S, A B$.
此时S在$l$上动，则A到B的变换为对合变换。

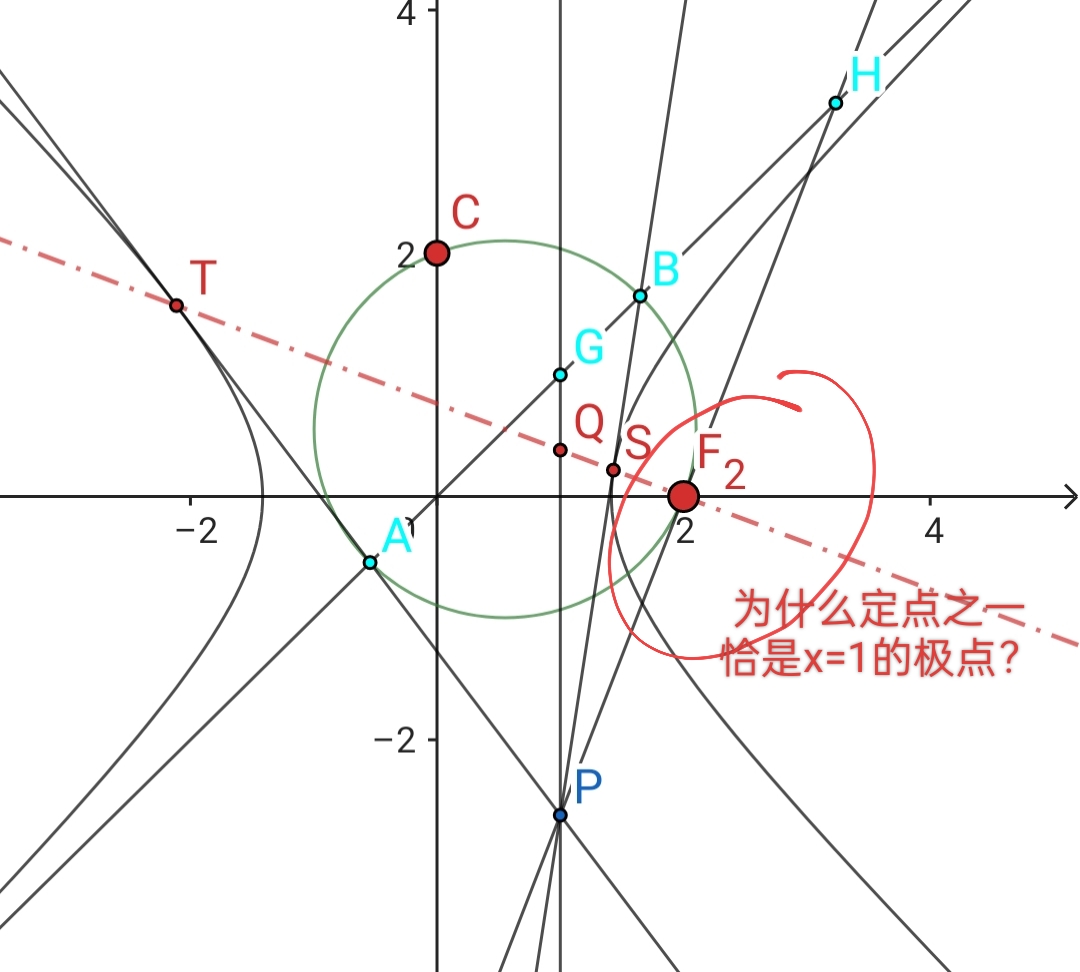
然而其关键原理的确是对合的乘幂，最后算出两定点之一恰好是x=1的极点。这是由命题人设置了特殊的系数所致还是隐藏着什么我没看出的原理？