$C(\theta) =\prod_{k=1}^\infty\sin(\theta/2^k)/(\theta/2^k)$

hbghlyj

设
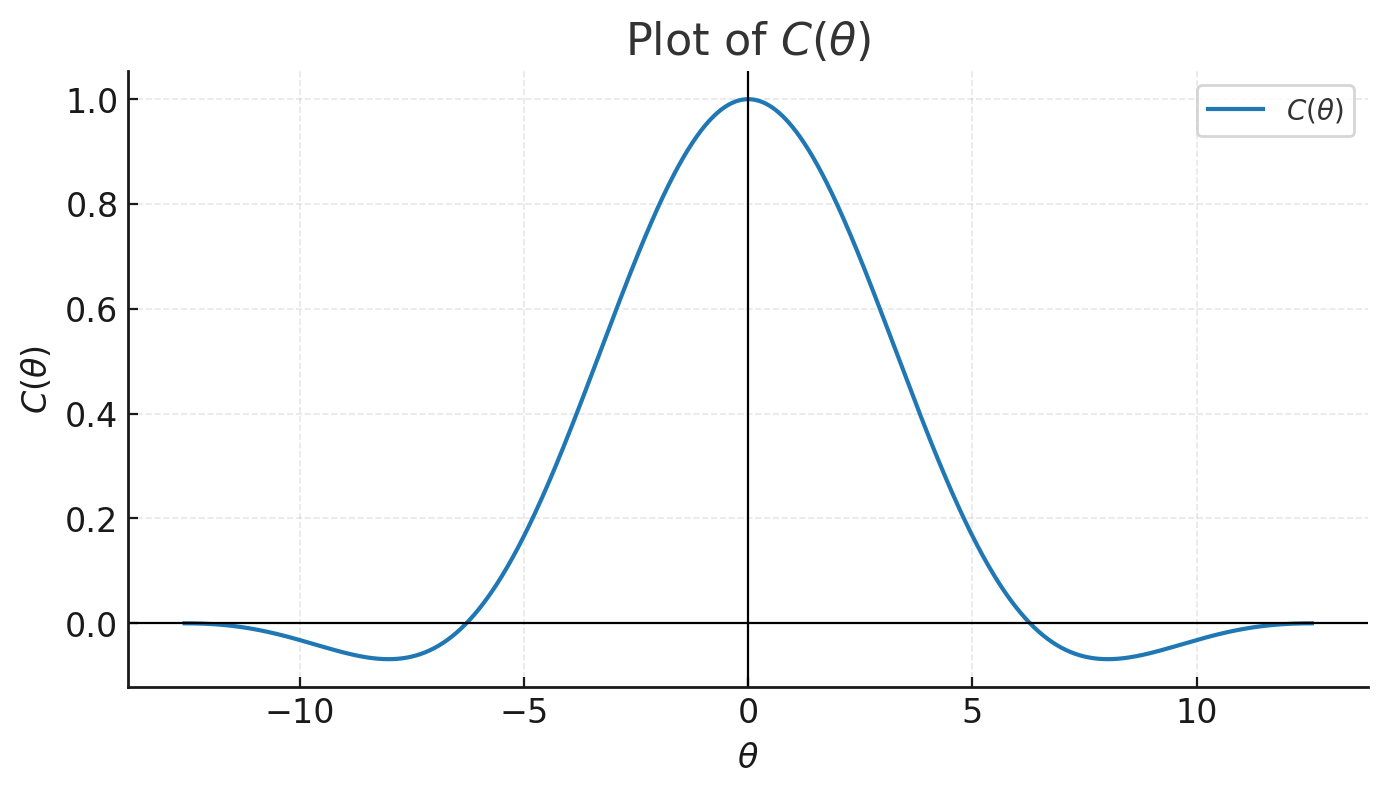
$$
C(\theta)=\prod_{k=1}^\infty \frac{\sin(\theta/2^k)}{\theta/2^k}.
$$求证：对于$\theta\notin 2\pi\mathbb Z$，有$0<|C(\theta)|<1$，例如$C(3\pi)\approx-0.0462$.

关于符号
如果$|\theta|<2\pi$，则每个$\sin(\theta/2^k)/(\theta/2^k)>0$，因此$0<C(\theta)<1$.
对于更大的$|\theta|$，只有有限多个因子可以是负的（那些满足$|\theta|/2^k\in(\pi,2\pi), (3\pi,4\pi),\dots$的因子），因此符号是$(-1)^{N(\theta)}$，其中$N(\theta)$计算那些负因子。这就是为什么$C(3\pi)<0$.

1. import numpy as np
2. import matplotlib.pyplot as plt
4. def C(theta, terms=50):
5.     result = 1.0
6.     for k in range(1, terms+1):
7.         x = theta / (2**k)
8.         if x != 0:
9.             result *= np.sin(x) / x
10.     return result
12. thetas = np.linspace(-4*np.pi, 4*np.pi, 1000)
13. values = [C(t) for t in thetas]
15. plt.figure(figsize=(8,4))
16. plt.plot(thetas, values, label=r"$C(\theta)$")
17. plt.axhline(0, color='black', lw=0.8)
18. plt.axvline(0, color='black', lw=0.8)
19. plt.title(r"Plot of $C(\theta)$")
20. plt.xlabel(r"$\theta$")
21. plt.ylabel(r"$C(\theta)$")
22. plt.grid(True, alpha=0.3)
23. plt.legend()
24. plt.show()

Copy the Code

hbghlyj

使用$\displaystyle \frac{\sin x}{x}=\prod_{j=1}^\infty \cos\big(x/2^j\big)$，
将双重乘积合并为单个乘积，并重新索引，（因为$k+j=m$的正整数$k,j$有$m-1$对）我们得到
$$
C(\theta)=\prod_{m=2}^\infty \Big(\cos\frac{\theta}{2^m}\Big)^{m-1}
$$
解析形式：通过$\log C$的幂级数
$$
\log C(\theta)=\sum_{n=1}^\infty a_n\,\theta^{2n},\quad
a_n=\frac{c_n\,2^{-4n}}{(1-2^{-2n})^2},
$$
其中$c_n$是$\log\cos x=\sum_{n\ge1} c_n x^{2n}$的系数（显式地，$c_n=-\,\dfrac{2^{2n}(2^{2n}-1)\,B_{2n}}{2n\,(2n)!}$，其中$B_{2n}$是伯努利数）。这为小的$|\theta|$提供了快速收敛的近似值。

• $C(\theta)$满足递归关系$C(\theta)=\dfrac{\sin(\theta/2)}{\theta/2}\,C(\theta/2)$。
• $C(0)=1$
• 如果$\theta$是非零的$2\pi$的倍数，则$C(\theta)=0$。
• 对于每个$\theta\notin 2\pi\mathbb Z$，有$0<|C(\theta)|<1$，例如$C(3\pi)\approx-0.0462$。

此外，当$|\theta|<2\pi$时，$C(\theta)>0$；对于更大的$|\theta|$，符号可以是负的。

hbghlyj

1) 除了$2\pi$的倍数外没有零点

一个因子$\sin(\theta/2^k)=0$，即$\theta= m\pi 2^k$，对于某个$k\ge1$ 这发生当且仅当$\theta\in 2\pi\mathbb Z$（因为当$k\ge1$时，$m$必须是偶数）。
因此，$C(\theta)=0$当且仅当$\theta\in 2\pi\mathbb Z$，否则没有因子为零。

2) 严格上界$|C(\theta)|<1$

对于任何实数$x\neq 0$，有$|\sin x|<|x|$。因此，每个因子的绝对值严格小于1。

3) 正下界（不坍缩到0）

选择足够大的$K$，使得$|\theta|/2^K\le 1$。对于$|x|\le 1$，有不等式
$$
\frac{\sin x}{x}\;\ge\;1-\frac{x^2}{6}.
$$
因此，对于$k\ge K$，
$$
\left|\frac{\sin(\theta/2^k)}{\theta/2^k}\right|
\ge1-\frac{\theta^2}{6\cdot 4^k}.
$$
因此
$$
|C(\theta)|≥\Bigg(\prod_{k=1}^{K-1}\left|\frac{\sin(\theta/2^k)}{\theta/2^k}\right|\Bigg)
\prod_{k=K}^{\infty}\left(1-\frac{\theta^2}{6\cdot 4^k}\right).
$$
第一个乘积是一个正数。第二个乘积每项在(0,1]中，且$\sum_{k=K}^{\infty}\frac{\theta^2}{6\cdot 4^k}<\infty,$因此它收敛到一个正极限（一个标准事实：如果$a_k\in[0,1)$且$\sum a_k<\infty$，则$\prod(1-a_k)>0$）。因此$|C(\theta)|>0$。