大家都来写一些关于 $\ln x$ 的不等式

realnumber

山西-宋xx
方程$\ln x=mx$有两个不等实数根$x_1,x_2$,求证：$(x_1+1)(x_2+1)> (e+1)^2$
分析：目标是证明$x_1x_2>e^2，1<x_1<e<x_2$,通过代入等式$\frac{\ln x_1}{x_1}=\frac{\ln x_2}{x_2}$,得到如下构造函数．
证明：设$f(x)=x^2(2-\ln x)-e^2\ln x,x\ge e$,$f(e)=0$
\[f'(x)=x(3-2\ln x-\frac{e^2}{x^2}),得f'(e)=0,\]
\[记g(x)=3-2\ln x-\frac{e^2}{x^2},x\ge e,g(e)=0\]
\[g'(x)=-\frac{2}{x}+\frac{2e^2}{x^3}=-\frac{2}{x^3}(x^2-e^2),\]
可见g(x)为减函数，得当$x>e,g(x)<g(e)=0$,即$f'(x)\le 0$
所以当$x>e$时,$f(x)<f(e)=0$,即$x^2(2-\ln x)-e^2\ln x<0,x>e$----(1)
假设$x_1x_2\le e^2,得x_1\le \frac{e^2}{x_2}<e$
由$h(x)=\frac{\ln x}{x},在(0,e)递增，(e,+∞)递减$
\[得到\frac{\ln x_1}{x_1}=\frac{\ln x_2}{x_2}\le \frac{\ln (\frac{e^2}{x_2})}{\frac{e^2}{x_2}}\]
\[即x_2^2(2-\ln x_2)-e^2\ln x_2\ge0,x_2>e与(1)矛盾．\]
即假设错误，因此有$x_1x_2\ge e^2$
那么$(x_1+1)(x_2+1)=x_1x_2+x_1+x_2+1>e^2+2e+1=(e+1)^2$.

realnumber

回复 21# realnumber

辽宁大连周亚明


我们的二模考试题

realnumber

[b]

其妙

这里也有应用：blog.sina.com.cn/s/blog_c2c533c30101hqm6.html
另外，作为资料，提一下本贴起源于这个帖子11-14楼：forum.php?mod=viewthread&tid=2515&ext … ;typeid=3&page=2

青青子衿

回复 24# 其妙
凑个热闹！
2004全国卷二
forum.php?mod=viewthread&tid=339
用琴生不等式

kuing

\[
\ln \left(1+\frac{1}{x}\right)<\frac{1}{\sqrt{x^2+x}}(x>0)
\]
有谁帮我证一下

\[
\begin{aligned}
& x=\frac{1}{u^2-1}, u>1, x^2+x=\frac{u^2}{\left(u^2-1\right)^2}, \\
& \ln \left(1+\frac{1}{x}\right)<\frac{1}{\sqrt{x^2+x}} \Leftrightarrow \ln \left(u^2\right)<\frac{u^2-1}{u} \\
& \Leftrightarrow \ln u<\frac{1}{2}\left(u-\frac{1}{u}\right)
\end{aligned}
\]

其妙

回复 26# kuing
啥子群哟，怎么没成司令？

kuing

回复 27# 其妙

一个广东教师群，我能有多少话可说，军长已经是我意料之外了……

血狼王

不废话，直接开火。
$$\ln x\geq \frac{8(x^3-1)}{3(x+1)^3}(x\geq 1)$$

kuing

不废话，直接开火。
$$\ln x\geq \frac{8(x^3-1)}{3(x+1)^3}(x\geq 1)$$
血狼王 发表于 2015-12-27 10:59

设 $f(x)=(1+x)^3\ln x$，当 $x>1$ 时，由泰勒展开有
\[f(x)=8(x-1)+8(x-1)^2+\frac83(x-1)^3+f^{(4)}(\xi)\frac{(x-1)^4}{4!},\]
其中 $\xi \in (1,x)$，不难计算出
\[f^{(4)}(x)=\frac{6(x-1)(x^2+1)}{x^4},\]
从而由 $\xi>1$ 得 $f^{(4)}(\xi)>0$，故
\[f(x)>8(x-1)+8(x-1)^2+\frac83(x-1)^3=\frac83(x^3-1),\]
即
\[\ln x>\frac{8(x^3-1)}{3(x+1)^3},\]
同时我们可以知道 $0<x<1$ 时不等式反向成立。

保留更多的项可以构造出反向式和更强式，只不过数据没这个好看。

敬畏数学

话说楼上y=lnx/x的图像是如何画出的？高手顺便解决，当m>1时，若关于x的方程mx=lnx+x有唯一零点，求m的取值范围？

kuing

皖A爱好者兰亭(1036******) 18:27:47
$x>0$, prove $\ln (x+1) \geq \frac{x}{\sqrt{1+x+\frac{x^2}{12}}}$
这个不等式怎么证明啊

这个比前面29#那个强，不过有了根式

kuing

回复 32# kuing

展开式有
\[\left(\frac x{\ln(x+1)}\right)^2=1+x+\frac{x^2}{12}-\frac{x^4}{240}+\frac{x^5}{240}-\cdots\]
不过计算应该比较复杂，直接求导来玩更容易计算些，令
\[f(x)=\ln(x+1)-\frac x{\sqrt{1+x+\frac{x^2}{12}}},\]
求导后最终可以化为
\[f'(x)=\frac{x^4(x^2+36x+36)}{(x+1)(x^2+12x+12)^{3/2} \bigl((x^2+12x+12)^{3/2}+12\sqrt3(x+1)(x+2)\bigr)},\]
故此……

isee

似乎和此楼的关系又不太大，只是说，存在$x>0$，类似于$0.5x^2-x<\ln x <x^2-x<2x^2-x$的不等式链成立。

kuing

好久没更新这帖了，刚才无意中在 forum.php?mod=redirect&goto=findpost& … d=6004&pid=30741 发现一个，记录一下：
当 `x\geqslant1` 时
\[\ln x\geqslant\frac{1-x^2+(x-1)\sqrt{x^2+34x+1}}{4x},\]当 `x\leqslant1` 时反向。

画图看了下应该是比 32# 更强，不过式子又更难看了……

或者这样变形下会好看点
\[\frac{\ln x}{x-1}>\frac{-x-1+\sqrt{x^2+34x+1}}{4x}=\frac8{x+1+\sqrt{x^2+34x+1}},\]上式对 `x\ne1` 成立。

也可以写成对数平均的形式，就是
\[\frac{a-b}{\ln a-\ln b}<\frac{a+b+\sqrt{a^2+34ab+b^2}}8,\]嗯，这样看起来还好些，不过变成这样之后，感觉这是个旧东西了……

======================
嗯，应该是没什么用了，好像还没这个强：
\[\frac{a-b}{\ln a-\ln b}<\frac{a+b+4\sqrt{ab}}6.\]

kuing

1. lst=Table[PadeApproximant[Log[x],{x,1,{m,n}}]//Factor,{n,0,4},{m,1,4}];
2. lst//TraditionalForm

Copy the Code

\[
\begin{array}{cccc}
x-1 & -\frac{1}{2} (x-3) (x-1) & \frac{1}{6} (x-1) \left(2 x^2-7 x+11\right) & -\frac{1}{12} (x-1) \left(3 x^3-13 x^2+23 x-25\right) \\
\frac{2 (x-1)}{x+1} & \frac{(x-1) (x+5)}{2 (2 x+1)} & -\frac{(x-1) \left(x^2-8 x-17\right)}{6 (3 x+1)} & \frac{(x-1) (x+1) \left(x^2-8 x+37\right)}{12 (4 x+1)} \\
-\frac{12 (x-1)}{x^2-8 x-5} & \frac{3 (x-1) (x+1)}{x^2+4 x+1} & \frac{(x-1) \left(x^2+19 x+10\right)}{3 \left(3 x^2+6 x+1\right)} & -\frac{(x-1) \left(x^3-15 x^2-123 x-43\right)}{12 \left(6 x^2+8 x+1\right)} \\
\frac{24 (x-1)}{x^3-5 x^2+19 x+9} & -\frac{3 (x-1) (19 x+11)}{(x+2) \left(x^2-26 x-5\right)} & \frac{(x-1) \left(11 x^2+38 x+11\right)}{3 (x+1) \left(x^2+8 x+1\right)} & \frac{(x-1) \left(3 x^3+131 x^2+239 x+47\right)}{12 \left(4 x^3+18 x^2+12 x+1\right)} \\
-\frac{720 (x-1)}{19 x^4-106 x^3+264 x^2-646 x-251} & \frac{90 (x-1) (27 x+11)}{11 x^4-104 x^3+1176 x^2+2056 x+281} & -\frac{10 (x-1) \left(136 x^2+271 x+55\right)}{3 \left(3 x^4-152 x^3-792 x^2-552 x-47\right)} & \frac{5 (x-1) (x+1) \left(5 x^2+32 x+5\right)}{6 \left(x^4+16 x^3+36 x^2+16 x+1\right)}
\end{array}
\]

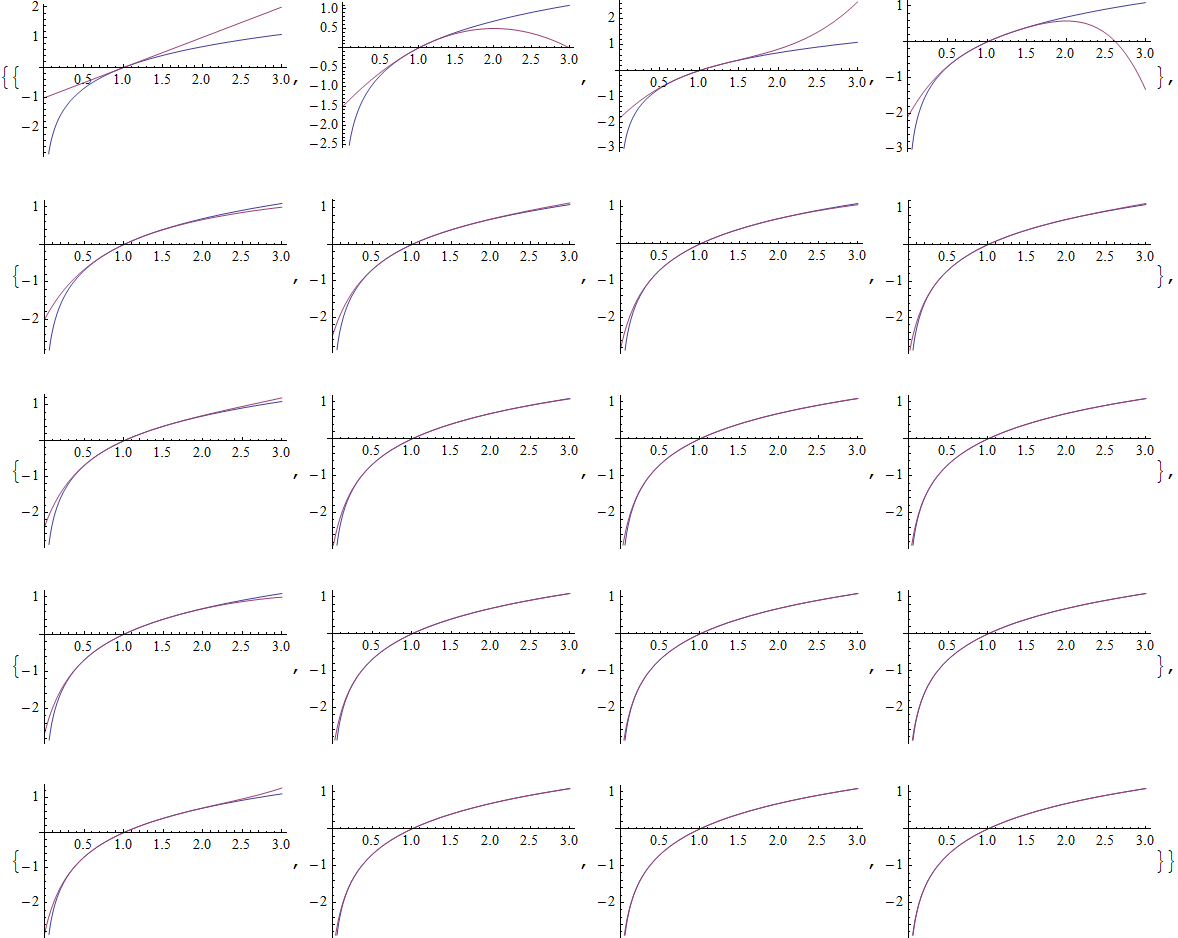
1. Table[Plot[{Log[x],lst[[n,m]]},{x,0,3}],{n,1,5},{m,1,4}]

Copy the Code

Czhang271828

回复 8# isee

搬运：目前这个精度$\log(1+x)\leq\dfrac{\pi+\frac{4+\pi}{2}\cdot x-2(x+2)\arctan\sqrt{x+1}}{\sqrt{1+x}}$

hbghlyj

kuing 发表于 2014-3-25 13:16
和第二个有点类似的
\[\ln x\geqslant 1-\frac1x, \forall x>0,\]
但其实它和第一个等价 ...

这个等价于 $\ln(1+x)\geqslant 1-\frac1{1+x}, \forall x>-1$
即$$\ln(1+x)\geqslant \frac{x}{1+x}, \forall x>-1$$
可以推广为：（当 $n=1$ 时，化为上式）$$\ln(1+x)\geqslant\sum_{i=1}^n \frac{x}{x i+n}, \forall x>-1$$

hbghlyj

hbghlyj 发表于 2024-4-3 09:22
可以推广为：（当 $n=1$ 时，化为上式）$$\ln(1+x)\geqslant\sum_{i=1}^n \frac{x}{x i+n}, \forall x>-1$$

1/x在[1,x]区间n等分的达布下和

WolframAlpha的证明：

好像什么也没说？