三角形中三点共线

乌贼

如图：
   
    在$ \triangle ABC $中，$ D,E $为$ AB $上任意两点，$ F,G $为$ AC $上任意两点，$ P $为$ EF $与$ DG $交点，$ M $为$ DC $与$ BF $交点，$ Q $为$ EC $与$ BG $交点。求证：（1）$ P,M,Q $三点共线；（2）什么情况下$ A,P,M,Q $四点共线。

isee

回复 1# 乌贼


    （1） 帕斯卡定理，就仅你这个，是帕普斯定理。

hbghlyj

帕普斯定理：ACE,BDF共线,AB∩DE=L,BC∩EF=M,CD∩FA=N,则LMN共线

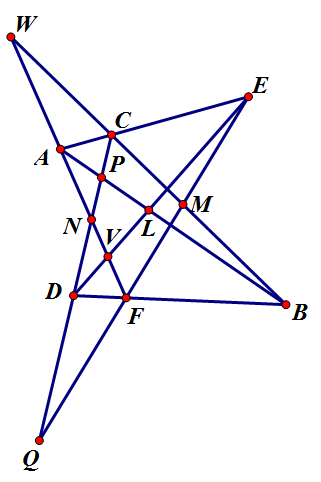
$(W,M,C,B)\overset{F}{\underset{\land}{=}}(N,Q,C,D)\overset{E}{\underset{\land}{=}}(N,F,A,V)\overset{D}{\underset{\land}{=}}(P,B,A,L)$
所以LMN共线
把上面的证明拆成梅涅劳斯定理：
MFQ截△BCD,$\frac{BM}{MC}\frac{CQ}{QD}\frac{DF}{FB}=1$
WFN截△BCD,$\frac{FB}{BW}\frac{WC}{DF}\frac{ND}{CN}=1$
DNP截△AVL,$\frac{PL}{PA}\frac{AN}{NV}\frac{VD}{DL}=1$
DFB截△AVL,$\frac{AB}{LB}\frac{LD}{DV}\frac{VF}{FA}=1$
DVE截△NQF,$\frac{QD}{ND}\frac{NV}{VF}\frac{FE}{EQ}=1$
ACE截△NQF,$\frac{CN}{CQ}\frac{QE}{EF}\frac{FA}{AN}=1$
WAN截△BCP,$\frac{CN}{NP}\frac{PA}{AB}\frac{BW}{WC}=1$
以上七式相乘得$\frac{BM}{MC}\frac{CN}{NP}\frac{PL}{LB}=1$
LMN截△BCP用梅涅劳斯逆定理，LMN共线
角元梅氏更简单：