主理想（principal ideal）

hbghlyj

bananaspace.org/wiki/主理想

wikipedia
环$ R $的理想$ I $称为主理想（principal ideal），若$ \exists \,a\in R:I=RaR=\left\{\sum _{i=1}^{n}r_{i}as_{i}:n\in \mathbb {N} ,r_{i},s_{i}\in R\,\forall \,i\right\} $

这个定义不同于

lectures17.pdf
Definition 46 Let $R$ be a ring and $a ∈ R$. Then the principal ideal $\langle a\rangle$ generated by $a$ is the smallest ideal to contain $a$. If $R$ has an identity $1_R$ then\[\langle a\rangle = \{ras : r, s ∈ R\} .\]

hbghlyj

Example 2.7.   In the ring $M_2 (\mathbb{F})$ put\[ A \coloneqq\left(\begin{array}{cc}        1 & 0\\        0 & 0      \end{array}\right) \text{ and } P \coloneqq\left(\begin{array}{cc}        0 & 1\\        1 & 0      \end{array}\right) \text{ so that } A + PAP = \left(\begin{array}{cc}        1 & 0\\        0 & 1      \end{array}\right) \] Then $1_2 = A + PAP \in \langle A \rangle$, but $A$ is not invertible so none of the matrices in $M_2 (\mathbb{F})$ is invertible, and hence $M_2   (\mathbb{F}) AM_2 (\mathbb{F})$ is not a subgroup and $\langle A \rangle   \neq M_2 (\mathbb{F}) AM_2 (\mathbb{F})$.  $\Box$ If there is $x \in R$ such that $I = \langle x \rangle$ then we say $I$ is principal and is generated by $x$. They are lines in vector space.

ringsandmodulespartsIandII

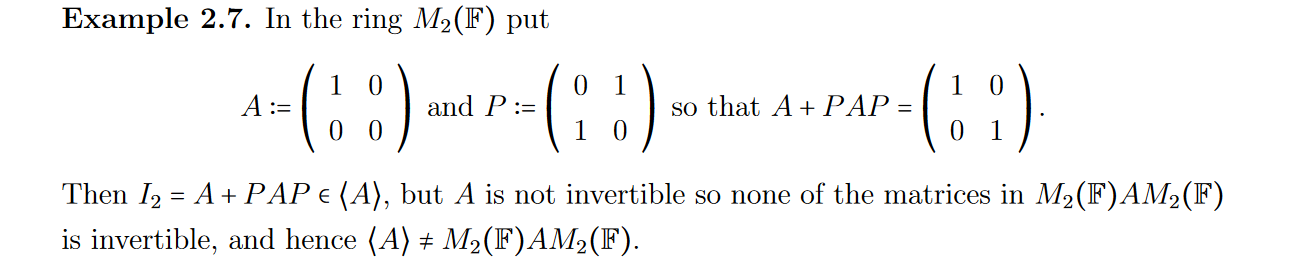
PS: 我发现LaTeX符 $+$, $=$, $\ne$, $\in$ 在此 pdf 中进行了修改(缩小)
PPS: 刚发现attachimg可以放在链接里(单击图像将转到 url)

Czhang271828

为什么 Definition 46 里定义的 $\langle a\rangle$ 是个理想?

按照二楼的例子, Definition 46 里定义的集合 $\langle a\rangle$ 包含所有秩 $\leq 1$ 的方阵, 但是这个集合对加法不封闭啊.