一道半圆内正方形，证线段相等

郝酒

BC是半圆的直径， D是半圆上任意一点，过D作DE⊥BC于E，在BC上取点F满足BF=BD，以EF为一边作正方形EFGH，连接BH并延长，交半圆于K，证明：GH=GK.

我能用坐标加三角算，但是感觉这题应该有背景，看上去KGO是共线的.

kuing

《撸题集》P.820 题目 6.2.6 似乎是这个的逆命题？

战巡

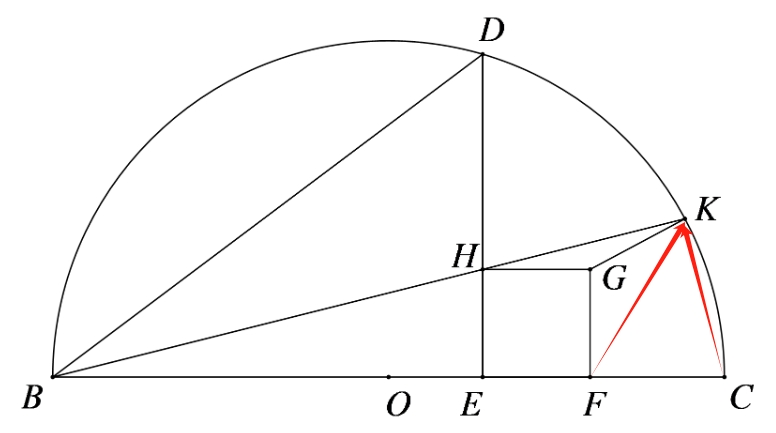
如图，连这两条线，不用去管什么$O, G, K$共不共线，那是另一个问题

令圆半径$R$，$BE=a$

于是
\[DE^2=OD^2-OE^2=R^2-(a-R)^2=2aR-a^2\]
\[BD=BF=\sqrt{DE^2+BE^2}=\sqrt{2aR-a^2+a^2}=\sqrt{2aR}\]
\[EF=EH=BF-BE=\sqrt{2aR}-a\]
\[CF=BC-BF=2R-\sqrt{2aR}\]

注意我们的目标，想要证明原题，其实只需要证明$\angle BKF=45\du$，又显然$\angle BKC=90\du$，即证明$KF$为$\angle BKC$平分线即可，然后由角平分线定理，可知需要证明：
\[\frac{BK}{KC}=\frac{BF}{CF}\]
这里面显然$\Delta BKC\sim\Delta BEH$，即
\[\frac{BK}{KC}=\frac{BE}{EH}=\frac{BE}{EF}\]
我们需要证明的东西，也就变成了
\[\frac{BE}{EF}=\frac{BF}{CF}\]
或者说
\[BE\cdot CF=EF\cdot BF\]
接下来就是计算了
\[BE\cdot CF=a\cdot(2R-\sqrt{2aR})=2aR-a\sqrt{2aR}\]
\[EF\cdot BF=(\sqrt{2aR}-a)\cdot\sqrt{2aR}=2aR-a\sqrt{2aR}\]
显然相等，于是完事

郝酒

谢谢两位，学习了.