证明垂直

史嘉

以△ABC的边BC为直径作半圆，于AB、AC分别交于Ｄ和Ｅ，过Ｄ，Ｅ作ＢＣ垂线，垂足分别为F,G，线段DG，EF交于点M，求证：AM⊥BC。

除了上解析法，用纯几何法或向量法怎么证明，请大侠出手。谢谢！

史嘉

回复 1# 史嘉


    哦，垂心？

kuing

见：
bbs.pep.com.cn/thread-393201-1-1.html
bbs.pep.com.cn/thread-671408-1-1.html

战巡

回复 1# 史嘉

同一法最简单了
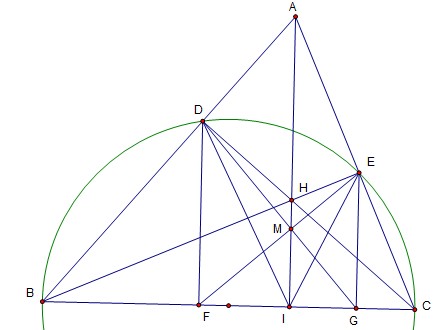
作直线$AH$交$BC$于$I$，与$DG$交于$M_1$，与$EF$交于$M_2$，其他连线如图
易证$AI⊥BC$，有：
\[\frac{IM_1}{DF}=\frac{IG}{FG}\]
\[\frac{IM_2}{EG}=\frac{IF}{FG}\]
证明$IM_1=IM_2$即可
于是有
\[\frac{IM_1}{IM_2}=\frac{IG·DF}{IF·EG}\]
而易证$B,I,H,D$共圆，$C,I,H,E$共圆，有$∠DIF=∠DHB=∠EHC=∠EIG$，$△DFI∽△EGI$
因此
\[\frac{IG·DF}{IF·EG}=1=\frac{IM_1}{IM_2}\]

kuing

回复 4# 战巡

3#的第二个链接你也证过一次

战巡

回复 5# kuing


死人kk翻链接翻的这么快

两个方法不太一样

史嘉

谢谢诸位，出手忒快！

isee

比主楼简单，差不多的弦切角小题。

题目：如图，已知$AB$是半圆$O$的直径，点$P$在半圆外的上方，且$PC$、$PD$分别与半圆相切于$C$、$D$两点。连接$AC$、$BD$交于一点$Q$。

求证：$PQ \perp AB$。

一种证明，以弦切角切入。(\wideparen AB 表示弧AB)


证明：延长$DP$至$H$，使$PH=DP$，又$PC=DP$,连$HC$，$CD$则$\angle DCH=90^\circ$。

于是需要证明的结论等价于

\[PQ \perp AB \iff \angle DQP+ \angle QBA=90^\circ  \iff  PD = PQ =PC\]

而由题，我们有：
\begin{align*}
\angle DQC&\stackrel{m}{=}\dfrac 12  (\wideparen {AB}+\wideparen{CD}) \\
  &\stackrel{m}{=}90^\circ +\dfrac 12  \wideparen{CD}\\[2em]
\angle H &= 90^\circ - \angle PCD\\
  &\stackrel{m}{=} 90^\circ - \dfrac 12  \wideparen{CD}\\[2em]
  \Rightarrow \angle DQC + \angle H &=180^\circ
\end{align*}

即有$D,Q,C,H$四点共圆，又$PH=PC=PD\Rightarrow PD=PQ=PC$，于是

\begin{align*}
\angle DQP+ \angle QBA&=\angle PDB + \angle DBA\\
  &\stackrel{m}{=} \dfrac 12  (\wideparen {BD}+\wideparen{DA}) \\
  &\stackrel{m}{=} \dfrac 12  \wideparen {AB}\\
  &=90^\circ\\[2em]
  \therefore PQ &\perp AB
\end{align*}

证毕。


PS：很久以前就见过，这题，在家长100论坛，看到不同的证明，又勾起了自己的回忆……

kuing

回复 8# isee

等号上面有个 m 是什么意思……

isee

回复 9# kuing


表弧的度数   

有多加m的，我改下。

第一章

回复  isee

等号上面有个 m 是什么意思……
kuing 发表于 2014-1-8 13:57

这个我懂，初中的老师讲过。不知道老师还健在否……

史嘉

回复 8# isee

好题！
红色字什么意思，弧长？

isee

回复 12# 史嘉

弧AB 之意。




另外的思路

isee

此两题能否统一，在高观点下，能不能给出一个统一的解释？

特别是后来的同一法证明，简直一模样

isee

回复 14# isee

我真傻瓜呀，原来 8楼 的P就是4楼 AH的中点，汗。

今天看到有人问P是AH的终于，突然明白过来

hbghlyj

华东师范大学出版社 数学奥林匹克小丛书•高中卷7:平面几何(第2版) 范端喜 邓博文 编著 page39

想看第三版, 但没有找到第三版的电子版, 只找到试读

另外:

isee 发表于 2014-1-8 05:03
(\wideparen AB 表示弧AB)

我在1#点评中把它\def了,现在8#的弧就能显示出来

色k

hbghlyj 发表于 2023-4-17 08:25
另外:
我在1#点评中把它\def了,现在8#的弧就能显示出来

还有这种操作😅