三个半圆和圆相切,求半径

hbghlyj

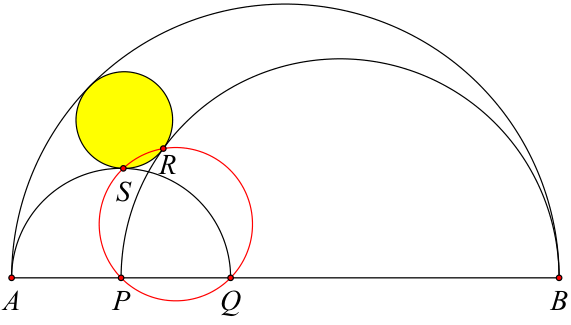
Problema 163.$r_1,r_2,R$是直径为AQ,PB和AB的半圆的半径,圆PQRS的半径为r,求证\[r^2=(r_1+r_2-R)^2+\frac{r_1r_2(R-r_1)(R-r_2)}{R^2}\]
(见2#,原题应该是打错了符号,把+打成了-)

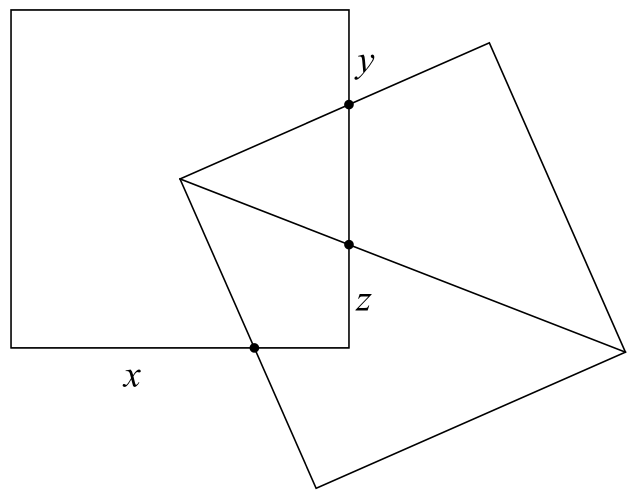
Problema 167.一个正方形的中心是另一个正方形的顶点,求证$y^2=x^2-2xz$.

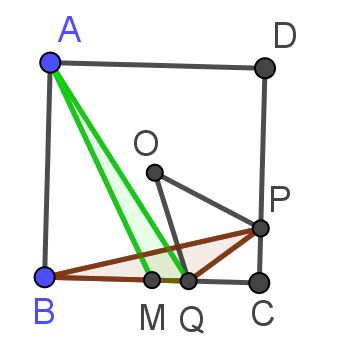
这等价于:正方形ABCD的中心为O,M为BC中点,P在CD上,Q在BC上,$\angle POQ=45\du$,求证$\S{AMQ}=\S{BPQ}$

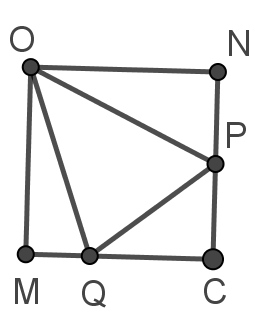
只看右下角的正方形OMCN,这等价于$2\S{OMQ}=\S{MPQ}+\S{PMC}$,而$\S{OMQ}+\S{ONP}=\S{OPQ},\S{OPN}+\S{MPC}=\S{OMP}$,化为$2\S{OPQ}=\S{MPQ}+\S{OPM}+\S{OPN}=\S{OMQ}+\S{ONP}+\S{OPQ}=2\S{OPQ}$,证毕!

原书:(Francisco Javier Garc ́ıa Capit ́an)Problemas y Soluciones-Volumen 1
书的大部分题目是用西班牙语写的,一小部分是英语.

kuing

Problema 163：
首先证明一下为什么 `PQRS` 一定共圆。

如图，设 `\triangle O_1O_2O_3` 的内心为 `I`，则由 `O_1Q=O_1S` 得 `IQ=IS`，同理有 `IP=IR` 以及 `IR=IS`，故 `IP=IQ=IR=IS`，从而 `PQRS` 四点共圆且圆心就是 `I`。

设圆 `O_3` 的半径为 `r_3`，记 `a=O_1O_2=2R-r_1-r_2`, `b=O_1O_3=r_1+r_3`, `c=O_2O_3=r_2+r_3`, `t=OO_3=R-r_3`, `u=OO_1=R-r_1`, `v=OO_2=R-r_2`，则由斯特瓦尔特定理，有 `b^2v+c^2u-t^2a=auv`，代入解得
\[r_3=\frac{R(R-r_1)(R-r_2)}{R^2-r_1r_2},\]设 `\triangle O_1O_2O_3` 的内切圆半径为 `r_n`，则
\[r_n^2=\frac{(a+b-c)(b+c-a)(c+a-b)}{4(a+b+c)},\]将前面的式子代入上式中化简得
\[r_n^2=\frac{r_1r_2(R-r_1)(R-r_2)}{R^2},\]又显然 `PQ=2r_1+2r_2-2R`，故所求的半径就是
\[r^2=\left(\frac{PQ}2\right)^2+r_n^2=(r_1+r_2-R)^2+\frac{r_1r_2(R-r_1)(R-r_2)}{R^2}.\]
所以原题应该是打错了符号，把 + 打成了 - 。

---

Problema 172：

如图所示，设那小段是 `x`，则在两个直角三角形中得
\begin{align*}
(R+x)^2+(r+h)^2&=(R+r)^2,\\
\left( R-\frac R{\sqrt2}+x \right)^2+(r+h)^2&=\left( \frac R{\sqrt2}-r \right)^2,
\end{align*}消 `x` 得
\[\bigl(2+\sqrt2\bigr)^2r^2+\bigl(4h+2\sqrt2R\bigr)r+2h^2-R^2=0,\]解之即得。

hbghlyj

Problema 168.$\overparen{GA}=\overparen{AB}=\overparen{BH}$,EH与FG是直径,GH与AE,BF交于C,D,求证CD+EF=4AB.
证:取EC中点M,则MO$\bot$NO,导角易得$\angle AON=\angle ANO$,所以A是MN中点,AB=MO=$\frac{EF+CD}4$.

hbghlyj

Problema 166.给定点A,B,正数k,$\vec{AC}=k\vec{CB},\vec{AD}=-k\vec{DB}$,O是AB中点,K是AB中垂线上任意一点,DK与以CD为直径的圆再交于N,N在AB上的投影为X,求证\[\frac{XN}{OK}=\frac k{(k-1)^2}\cdot\frac{AB^2}{DK^2}\]也就是\[\frac{DN⋅DK}{AB^2}=\frac k{(k-1)^2}\],而DN⋅DK=DC⋅DO=DA⋅DB,剩下的是显然的.

2375319874

易得$ \vec{EF} $
$ \vec{GH} $$ \px  $AB，导角得$ \alpha $相等，得平行四边形ABFK，ABJE，
$ \triangle $ GON$ \cong $$ \triangle $ BON，$ \beta $ 相等，得平行四边形
ABGN，由对称性JO=OH=OK，HK$ \perp  $EF→EK=HG，.EG=CN..JK=GC\\.EF+GH=EJ+JK+KF+DN+CN=3AB
+GN=4AB