极坐标 平移

hbghlyj

圆 $$r=a$$ 将原点平移到点$(r_p,0)$变为 $$r = r_p \cos\theta + \sqrt{a^2 - r_p^2 \sin^2\theta}$$

---

四叶草(quatrefoil) $$r=\cos2\theta$$ 将原点平移到点$(1,0)$变为 $$2 r^5-12 r^4 \cos\theta+r^3 (12 \cos 2\theta-\cos 4\theta+17)-32 r^2 \cos\theta+r (4 \cos 2\theta+14)-4 \cos\theta=0$$

eqn=14 r+17 r^3+2 r^5-4 Cos[t]-32 r^2 Cos[t]-12 r^4 Cos[t]+4 r Cos[2 t]+12 r^3 Cos[2 t]-r^3 Cos[4 t]==0;
PolarPlot[{r/.Solve[eqn,r][[1]],
           r/.Solve[eqn,r][[2]],
           r/.Solve[eqn,r][[3]],
           r/.Solve[eqn,r][[4]],
           r/.Solve[eqn,r][[5]]},{t,0,Pi}]

分为五段, 用颜色区分:

hbghlyj

分界点是什么呢

其中,四个分界点是

{{Root[25 - 42*#1 + 11*#1^2 + 4*#1^3 & , 3, 0], Root[20 - 316*#1^2 + 333*#1^4 + 16*#1^6 & , 2, 0]}, 
 {Root[25 - 42*#1 + 11*#1^2 + 4*#1^3 & , 2, 0], Root[20 - 316*#1^2 + 333*#1^4 + 16*#1^6 & , 1, 0]}, 
 {Root[25 - 42*#1 + 11*#1^2 + 4*#1^3 & , 2, 0], Root[20 - 316*#1^2 + 333*#1^4 + 16*#1^6 & , 4, 0]}, 
 {Root[25 - 42*#1 + 11*#1^2 + 4*#1^3 & , 3, 0], Root[20 - 316*#1^2 + 333*#1^4 + 16*#1^6 & , 3, 0]}}

数值:

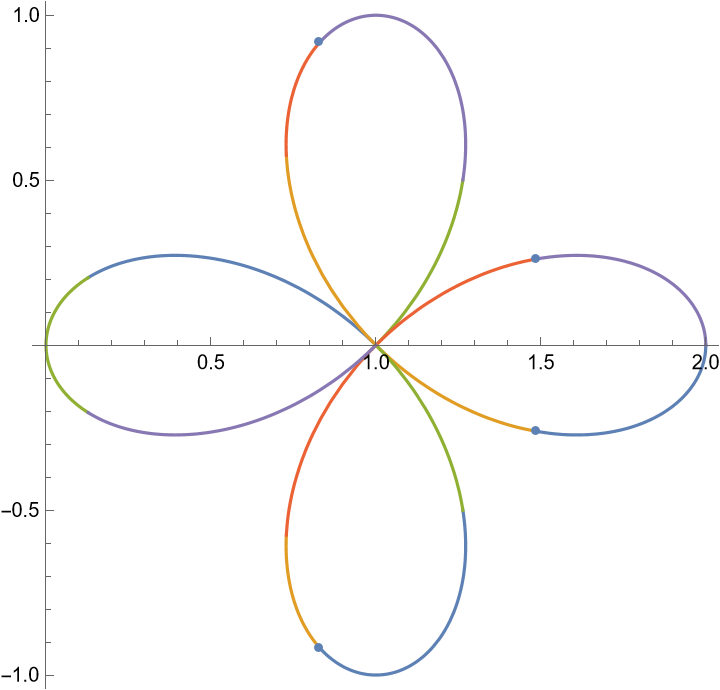
{{1.4857862556160124, -0.26117068908747654}, {0.8303263858128664, -0.9184551949565968}, 
 {0.8303263858128664, 0.9184551949565968}, {1.4857862556160124, 0.26117068908747654}}

hbghlyj

desmos-graph-1.svg (5.85 KB, Downloads: 73)

2022-8-23 07:53 Upload

Click on the file to download the attachment

$$r=2\cos\theta+\sqrt{2-4\left(\sin\theta\right)^{2}}$$红色: $0\le\theta\le\pi$
绿色: $\pi\le\theta\le2\pi$
分界点是$(2\pm\sqrt2,0)$和(过$O$的切线的切点)$(1,\pm1)$.