张角定理、极坐标下的直线两点式、同焦同准圆锥曲线一命题

kuing

张角定理，是平面几何学的一个定理，指任意 `\triangle ABC` 中，`D` 是边 `BC`（包括端点）上的点，连接 `AD`，则
\[\frac{\sin\angle BAD}{AC}+\frac{\sin\angle CAD}{AB}=\frac{\sin\angle BAC}{AD},\]
其逆定理亦成立。

以上摘自维基，但其实只要将角 `\angle` 改为有向角 `\measuredangle`，字母的顺序调整下，那么 `D` 亦可在 `BC` 延长线上。

写成轮换对称的形式，即：若三点 `P_1`, `P_2`, `P_3` 共线，`O` 在直线外，则有
\[\frac{\sin\measuredangle P_1OP_2}{OP_3}+\frac{\sin\measuredangle P_2OP_3}{OP_1}+\frac{\sin\measuredangle P_3OP_1}{OP_2}=0.\]

由此即得极坐标下的两点式：设极坐标下两点 `A(\rho_1,\theta_1)`, `B(\rho_2,\theta_2)`，则直线 `AB` 的方程为
\[\frac{\sin(\theta_1-\theta_2)}\rho+\frac{\sin(\theta_2-\theta)}{\rho_1}+\frac{\sin(\theta-\theta_1)}{\rho_2}=0.\]

我不会无缘无故写这些，话说前两天研究某微信网友的一类问题时发现以下的：

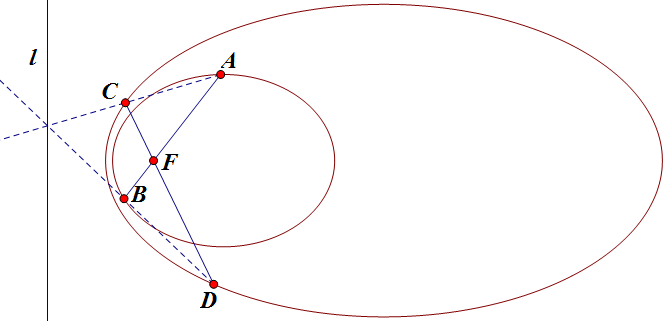
命题：已知两圆锥曲线 `\Gamma_1`, `\Gamma_2` 有共同的焦点 `F` 及准线 `l`，`\Gamma_1` 上的弦 `AB` 过 `F`，`\Gamma_2` 上的弦 `CD` 过 `F`，则直线 `AC` 与 `BD` 的交点在 `l` 上。

此题利用上述两点式以及圆锥曲线的极坐标方程，证起来就计算量就不大。

证明：只需证明 `AC` 与 `l` 的交点与 `BD` 与 `l` 的交点是同一个点即可。

记焦准距为 `p`，建立极坐标系使 `F` 为原点且准线为 `\rho\cos\theta=-p`。

设 `\Gamma_1`, `\Gamma_2` 的离心率分别为 `e_1`, `e_2`，则可设 `A(\rho_1,\theta_1)`, `C(\rho_2,\theta_2)`，其中
\[\rho_1=\frac{e_1p}{1-e_1\cos\theta_1},~\rho_2=\frac{e_2p}{1-e_2\cos\theta_2},\]
根据上述两点式，可知直线 `AC` 的方程为
\[\frac{\sin(\theta_1-\theta_2)}\rho+\frac{\sin(\theta_2-\theta)(1-e_1\cos\theta_1)}{e_1p}+\frac{\sin(\theta-\theta_1)(1-e_2\cos\theta_2)}{e_2p}=0,\]
（注意别看错了 `\rho` 与 `p`）整理为
\[\frac{\sin(\theta_1-\theta_2)}\rho+\frac{\sin(\theta_2-\theta)}{e_1p}+\frac{\sin(\theta-\theta_1)}{e_2p}-\frac{\sin(\theta_2-\theta)\cos\theta_1+\sin(\theta-\theta_1)\cos\theta_2}p=0,\]
易证恒等式 `\sum\sin(x-y)\cos z=0`，则 `\sin(\theta_2-\theta)\cos\theta_1+\sin(\theta-\theta_1)\cos\theta_2=-\sin(\theta_1-\theta_2)\cos\theta`，所以 `AC` 的方程最终化简为
\[\sin(\theta_1-\theta_2)\left(\frac p\rho+\cos\theta\right)+\frac{\sin(\theta_2-\theta)}{e_1}+\frac{\sin(\theta-\theta_1)}{e_2}=0,\]
而准线 `l` 的方程为
\[\rho\cos\theta=-p,\]
联立以上两方程，后者代入前者消去 `\rho`，恰好第一项就没了，得到
\[\frac{\sin(\theta_2-\theta)}{e_1}+\frac{\sin(\theta-\theta_1)}{e_2}=0,\]
去分母展开即
\begin{gather*}
e_1\sin(\theta-\theta_1)=e_2\sin(\theta-\theta_2),\\
e_1(\sin\theta\cos\theta_1-\cos\theta\sin\theta_1)=e_2(\sin\theta\cos\theta_2-\cos\theta\sin\theta_2),\\
e_1(\tan\theta\cos\theta_1-\sin\theta_1)=e_2(\tan\theta\cos\theta_2-\sin\theta_2),\\
\tan\theta=\frac{e_1\sin\theta_1-e_2\sin\theta_2}{e_1\cos\theta_1-e_2\cos\theta_2},\quad(*)
\end{gather*}
这便是 `AC` 与 `l` 的交点的极角 `\theta` 满足的等式。

至于 `BD`，显然 `B`, `D` 的极角分别就是 `A`, `C` 的 `\theta_1`, `\theta_2` 变成 `\theta_1+\pi`, `\theta_2+\pi`，再看式 (*)，显然 `(\theta_1,\theta_2)\to(\theta_1+\pi,\theta_2+\pi)` 后右边的值不变，这就说明了 `BD` 与 `l` 的交点与 `AC` 与 `l` 的交点是同一点，即命题得证。

lemondian

这个东东能不能用来证明：kuing.cjhb.site/forum.php?mod=viewthread&tid=13230
1#的命题？

abababa

主楼的原问题应该好证明，maven以前给我讲过，对于共焦共准的两个圆锥曲线，存在一个射影变换把这两个曲线映到同心圆，把共同的焦点$F$映到圆心，把共同的准线$\ell$映到无穷远。

这样作完映射之后，就有$\triangle FAC\cong\triangle FBD$，进而得到$AC\sslash BD$，所以交点就在无穷远线$\ell$上，那变换前的交点也在$\ell$上。

abababa

abababa 发表于 2025-4-4 15:13
主楼的原问题应该好证明，maven以前给我讲过，对于共焦共准的两个圆锥曲线，存在一个射影变换把这两个曲线 ...

以前没学线性代数时，这个射影变换我看不懂，只是看别人说存在，就记下来了，觉得有用。后来我学了一点线性代数，所说的射影变换其实就是一个三阶可逆方阵，向量就表示点，例如$\begin{bmatrix}x\\y\\1\end{bmatrix}$，表示直角坐标系下的点$(x,y)$，第三个分量1是齐次化用的，maven喜欢用一般的字母z表示，我还是习惯用1表示。

直线$Ax+By+C=0$也可以用矩阵形式来表示，就是
\[
\begin{bmatrix}A\\B\\C\end{bmatrix}^T
\begin{bmatrix}x\\y\\1\end{bmatrix}=0
\]

然后一个圆锥曲线，它其实就是一个关于$x,y$（齐次化后还有$z$）的二元二次方程$Ax^2+2Bxy+Cy^2+2Dx+2Ey+F=0$。它还能表示成矩阵的形式：
\[
\begin{bmatrix} x & y & 1\end{bmatrix}
\begin{bmatrix}
A & B & D\\
B & C & E\\
D & E & F
\end{bmatrix}
\begin{bmatrix}
x\\y\\1
\end{bmatrix}=0
\]
这样的话，一个圆锥曲线其实就对应了一个三阶矩阵。

一个射影变换$H$，把一个点$X=(x,y,1)^T$（^T表示转置）变为$HX$，就是把矩阵作用在向量上。

现在回到3楼所说的那个射影变换，为了简单，不妨设焦点$F=(0,0)$，齐次化后$F=(0,0,1)$，准线为$\ell: x=\lambda$，设$\Gamma_1,\Gamma_2$的离心率分别为$e_1,e_2$。由圆锥曲线的定义知，点$(x,y)$到焦点$F=(0,0)$的距离与到准线$1x+0y-\lambda=0$的距离之比等于离心率$e_i$，即$\Gamma_i: \sqrt{(x-0)^2+(y-0)^2}=\frac{e_i\abs{1x+0y-\lambda}}{1^2+0^2}$，即$x^2+y^2=(e_i\abs{x-\lambda})^2$，写为矩形形式即为
\[
\begin{bmatrix}
x & y & 1
\end{bmatrix}
\begin{bmatrix}
1-e_i^2 & 0 & \lambda e_i^2\\
0 & 1 & 0\\
\lambda e_i^2 & 0 & -\lambda^2e_i^2
\end{bmatrix}
\begin{bmatrix}
x \\ y \\ 1
\end{bmatrix}=0
\]

把中间的那个矩阵取出来，就是两个圆锥曲线对应的矩阵，设
\[
Q_i=
\begin{bmatrix}
1-e_i^2 & 0 & \lambda e_i^2\\
0 & 1 & 0\\
\lambda e_i^2 & 0 & -\lambda^2e_i^2
\end{bmatrix}
\]

令射影变换为
\[
H=
\begin{bmatrix}
\frac{1}{\lambda} & 0 & 0\\
0 & 1 & 0\\
\frac{1}{\lambda} & 0 & -1
\end{bmatrix}
\]

经软件计算，$H$是可逆的。

点$F$在$H$的作用下就变为$HF=(0,0,-1)$，还表示点$(0,0)$，也就是说$H$把$F$仍变为$F$。然后看准线$1x+0y-\lambda=0$，写成矩阵形式就是$(1,0,-\lambda)^TX=0$，而这个直线上的点$X$在$H$的作用下变为$Y=HX$，所以$X=H^{-1}Y$，代入就有$(1,0,-\lambda)^TH^{-1}Y=0$，$(1,0,-\lambda)^TH^{-1}=(0,0,\lambda)=(0,0,1)$，所以变换后的直线方程是$(0,0,1)^TY=0$，就是无穷远线。然后是那两个圆锥曲线，圆锥曲线的方程为$X^TQ_iX=0$，射影变换矩阵$H$将点$X$映为$Y$，所以$Y=HX$，从而$X=H^{-1}Y$，代入原方程即有$(H^{-1}Y)^TQ_i(H^{-1}Y)=0$，也即$Y^T(H^{-T}Q_iH^{-1})Y=0$，所以新的圆锥曲线的矩阵为$H^{-T}Q_iH^{-1}$，其中$H^{-T}$表示$H^{-1}$的转置矩阵。然后用软件计算这个$H^{-T}Q_iH^{-1}$，就是
\[
\begin{bmatrix}
\lambda^2 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & -\lambda^2 e_i^2\\
\end{bmatrix}
\]

写成通常的方程（其中用$Y=(y_1,y_1,1)^T$来表示$Y$）就是$\lambda^2y_1^2+y_2^2=\lambda^2e_i^2$，通过选择坐标刻度，可以使$\lambda=1$，这样最终变换后的这两个曲线就是圆了。

不过这个不变成圆也应该可以，最后变成了同心的椭圆，两个三角形还是对称的，通过全等和角度就有那两个边平行，还是交于无穷远点（在无穷远线上）。

lxz2336831534

如图，设共焦点为F，直线HK,IJ分别和准线交于O,L.
易知(OFHK)=(LFJI)=-1
所以点对F,O、F,L关于过H,I,J,K四点的圆锥曲线共轭
则点F和直线OL上的所有点关于HIJK圆锥曲线共轭
也即点F关于过HIJK四点的圆锥曲线的极线是OL
根据完全四点形HIJK的调和性质，易知HI，KJ的交点在点F的极线上

lxz2336831534

lxz2336831534 发表于 2025-4-11 09:00
如图，设共焦点为F，直线HK,IJ分别和准线交于O,L.
易知(OFHK)=(LFJI)=-1
所以点对F,O、F,L关于过H,I,J,K四 ...

另外，过HIJK四点的二次曲线系与x轴的两个交点属于一个对合变换，该对合变换被点F和直线OL所确定。

lxz2336831534

forum.php?mod=viewthread&tid=13697 此题第三问是更普通的问题，当广义根轴重合时即退化为共焦点共准线问题