三角形之内切圆

乌贼

最近看了几道三角形内切圆题目，发觉其博大精深，也接触极点极线，这里主要收集资料及例题，并从初等几何方面看看作作，权当学习方家莫笑，也希望大家指点。

概念链接：
     baike.baidu.com/link?url=70cjs_SIYHGFKBL1LM-R … uPP-FtBkuqOUuk4MHK7K
性质链接：
    ziyuan.wmw.cn/WLKT/LWMWMZ/RJB/classonline/con … 11/html/274hb_16.htm
待续……

zhcosin

可以参考这个
en.wikipedia.org/wiki/Incircle_and_excircles_of_a_triangle

乌贼

回复 2# zhcosin
谢谢，英文，慢慢看。

乌贼

$ \triangle ABC $中，$ D,E,F $分别为内切圆$ I $在$ BC,AC,AB $上的切点，$ H $为$ \triangle ABC $的垂心，$ Q $为$ A $点在$ BC $上的垂足，$ DP\perp EF $于$ P $。求证：$ \angle IPD=\angle DPH=\angle DIQ $

乌贼

一些结论：
1.$ \triangle ABC $内切圆$ I $对应边$ BC,CA,AB $上的切点分别为$ D,E,F $，$ DP\perp FE $于$ P $，$ AQ $为$ \triangle ABC $外接圆直径，则$ P,I,Q $三点共线。

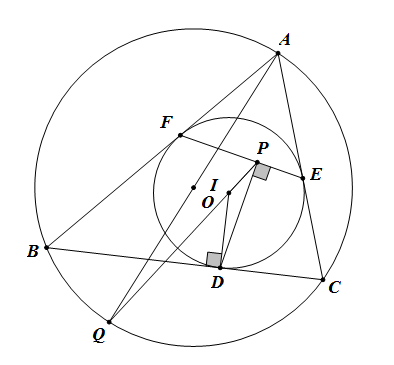
2.$ \triangle ABC $内切圆$ I $对应边$ BC,CA,AB $上的切点分别为$ D,E,F $，$ DP\perp FE $于$ P $，$ AQ\perp BC $于$ Q $，$ H $为$ \triangle ABC $垂心，$ IQ $延长线交$ \triangle PID $外接圆于$ K $点。则$ P,H,K $三点共线。

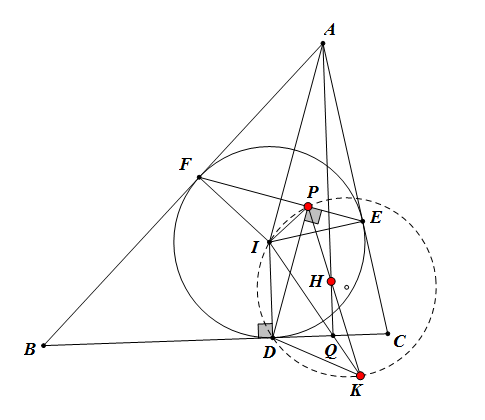
3.$ \triangle ABC $内切圆$ I $对应边$ BC，AC，AB $上的切点分别为$ D，E，F $，$ DE $与$BA $的延长线交于点$ P $。则$ PI\perp FC $

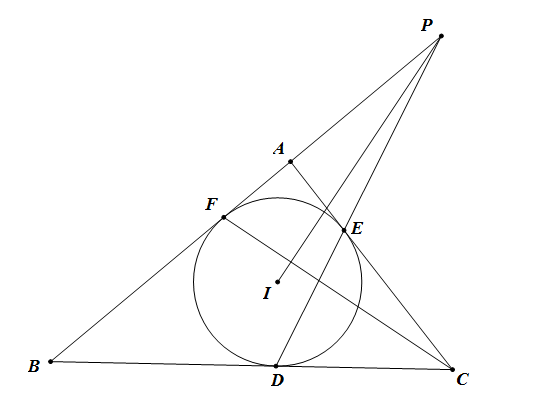
4.$ I $为$ \triangle ABC $内心，$ AI $延长线交$ BC $于$ D $，$ BI $延长线交$ AC $于$ E $，$ DE $与$ BA $的延长线交于点$ P $。则$ PC\perp IC $

乌贼

链接：kuing.cjhb.site/forum.php?mod=viewthread& … 1&extra=page%3D1

hbghlyj

1
14
2600(djc)，内切圆配极专题(度量篇)
内切圆配极专题汇总
简单的内心汇总
3404
4079
4258
4473

hbghlyj

四边形ABCD内接于圆$\Gamma$,$I_1,I_2$分别是△ABC,△DBC的内心,M是$\Gamma$中弧BC的中点.$\Omega$是与$BI_1,CI_2,\Gamma$相切的圆,求证:$\triangle I_1I_2M$的外接圆与$\Omega$相切.

乌贼

回复 9# hbghlyj
纯几何吧我只看不作

乌贼

回复 5# 乌贼
题3
如图：
$ L $为$ PI $与$ CF $的交点，连接$ IC $交$ DE $于$ Q $，连接$ FI，DI，FQ $。有\[ \triangle DQI\sim \triangle CDI\riff ID^2=IQ\cdot IC\riff IF^2=IQ\cdot IC\riff \triangle FIQ\sim \triangle CIF\\\riff \angle ICF=\angle IFQ \]又$ FIQP $四点共园，得\[ \angle ICF=\angle IFQ=\angle IPQ \]所以$ CQLP $四点共园，即\[ \angle PLC=\angle PQC=90\du  \]

hbghlyj

回复 12# 乌贼
证明:C的极线DE经过P,F的极线AB极线AB经过P,所以CF是P的极线,所以PI⊥FC.

hbghlyj

回复 5# 乌贼
4.证明:对完全四边形AECDBI有CD,CE调和分割CI,CP,所以CP是外角平分线,所以PC⊥IC.

乌贼

kuing.cjhb.site/forum.php?mod=viewthread&tid=7370

乌贼

tieba.baidu.com/p/6091232656?pn=1

isee

回复 16# 乌贼

建议先读读《高等几何》，如果线性代数忘得差不多了，就看朱德祥，朱维宗编的，有PDF的。

如果不想那么深入，看下《近代欧氏几何》亦可，单壿译的，这也是鸿篇巨制~

再不济就读读《几何变换与几何证题》，萧振纲著，相关章节是 反演变换

或者随便网上看看调和点列及应用，总之，这块东西实在是太多了，且有趣，且易忘记，哈哈哈哈哈

乌贼

回复 17# isee


功力不够，怕走火入魔。先学习调和极线级点。

isee

回复 18# 乌贼

高等几何里全有哇，就是高等几何研究的对象，系列讲的，不会走的

乌贼

kuing.cjhb.site/forum.php?mod=viewthread& … 0&extra=page%3D1

hbghlyj

可以建立一个淘专辑

hbghlyj

AOPS
Geometry Unbound Problems for Section 11.5

Let $I$ be the incenter of triangle $ABC$. Let $K,L$ and $M$ be the points of tangency of the incircle of $ABC$ with $AB,BC$ and $CA$, respectively. The line $t$ passes through $B$ and is parallel to $KL$. The lines $MK$ and $ML$ intersect $t$ at the points $R$ and $S$. Prove that $\angle RIS$ is acute.
Evan Chen, §2.2 IMO 1998/5

First simple proof (grobber)
The problem is equivalent to showing $BI^2 > BR \cdot BS$.
But from
\[ \triangle BRK \sim \triangle MKL \sim \triangle BLS \]
we conclude
\[ BR = t \cdot \frac{MK}{ML},
  \qquad BS = t \cdot \frac{ML}{MK} \]
where $t = BK  = BL$ is the length of the tangent from $B$.
Hence $BR \cdot BS = t^2$.
Since $BI > t$ is clear, we are done.

Second projective proof
Let $N$ be the midpoint of $\overline{KL}$, and let ray $MN$ meet the incircle again at $P$.

Note that line $\overline{RBS}$ is the polar of $N$.
By Brokard's theorem, lines $MK$ and $PL$ should thus meet the polar of $N$, so we conclude $R = \overline{MK} \cap \overline{PL}$.
Analogously, $S = \overline{ML} \cap \overline{PK}$.

Again by Brokard's theorem, $\triangle NRS$ is self-polar, so $N$ is the orthocenter of $\triangle RIS$.
Since $N$ lies between $I$ and $B$ we are done.