直角三角形周长为1，求面积最大值

isee

源自知乎提问

---

题：在三角形 ABC 中，若 $C=\pi/2$ 且 $2p=a+b+c=1$ ，求三角形 ABC 面积 $S_{\triangle}$ 的最大值.

---

如图 1，三角形 ABC 的内切圆半径为 r，则 \begin{gather*}
\tan \frac A2=\frac{r}{p-a}=\frac{S_{\triangle}}{p(p-a)},
\end{gather*}

图 1

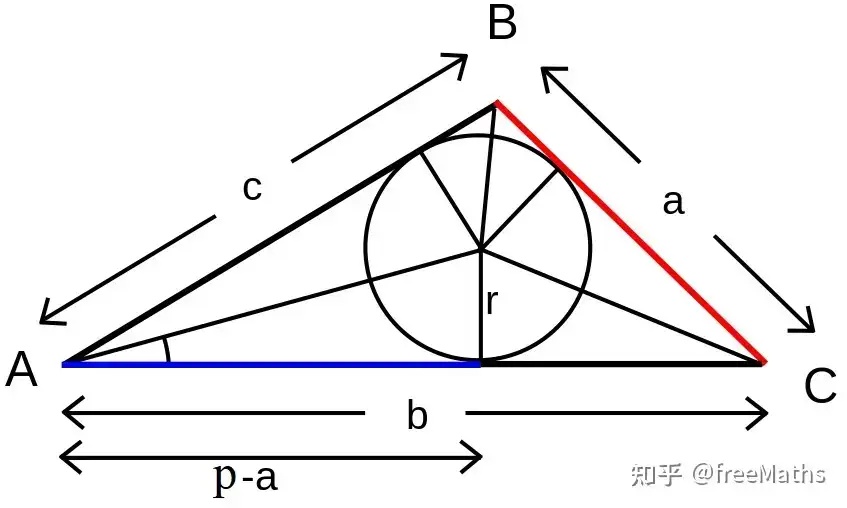
分别轮换 a，b，c 与 A，B，C 就有 \begin{gather*}
\tan \frac A2\tan \frac B2\tan \frac C2=\frac{S_{\triangle}^2}{p(p-a)(p-b)(p-c)}\cdot \frac{S_{\triangle}}{p^2},\\[1ex]
\iff {\color{blue}{S_{\triangle}=p^2\tan \frac A2\tan \frac B2\tan \frac C2}}.
\end{gather*} 这就得到了三角形的一个面积公式（其过程用到了 $S_{\triangle}=pr=\sqrt{p(p-a)(p-b)(p-c)}$ 这两个基本公式），代入直角条件即有 \begin{gather*}
S_{\triangle}=p^2\tan \frac A2\tan \frac B2.
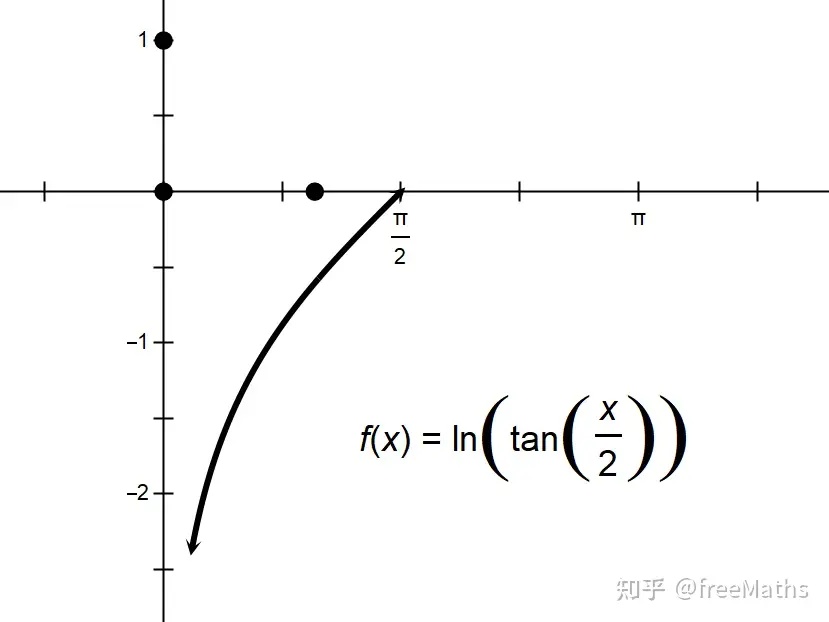
\end{gather*} 注意到函数 $f(x)=\ln\left(\tan\frac x2\right),\ x\in(0,\pi/2)$ ， $f''(x)=\frac14\left(\sec^2\frac x2-\csc^2\frac x2\right)<0$ 即 $f(x)$ 在 $(0,\pi/2)$ 为上凸函数，如图 2.

图 2

由 Jensen 不等式 \begin{gather*}
\frac12f\left(\frac A2\right)+\frac12f\left(\frac B2\right)\leqslant f\left(\frac{A/2+B/2}2\right),\\[1ex]
\iff {\color{blue}{\frac12\ln\tan\frac A2+\frac12\ln\tan\frac B2\leqslant \ln\tan\frac{\pi}8}}\\[1ex]
\iff \tan\frac A2\tan\frac B2\leqslant \left(\tan\frac{\pi}8\right)^2=3-2\sqrt2.
\end{gather*} 如此一来 \begin{gather*}
S_{\triangle}=p^2\tan \frac A2\tan \frac B2\leqslant\frac{3-2\sqrt2}4,
\end{gather*} 当且仅当三角形 ABC 为等腰直角三角形时取得等号.

kuing

后半竟然用琴生😂是故意秀的吗？

如果是我就
\begin{gather*}
\tan\frac A2\tan\frac B2=1-\tan\frac A2-\tan\frac B2\leqslant1-2\sqrt{\tan\frac A2\tan\frac B2}\\
\riff\tan\frac A2\tan\frac B2\leqslant3-2\sqrt2.
\end{gather*}