应该是摆线吧心脏线

isee

2025届广州一模，多选压轴

如图，半径为 1 的动圆 C 沿着圆 $O:x^2+y^2=1$ 外侧无滑动地滚动一周，圆 C 上的点 $P(a,b)$ 形成的外旋轮线 $Γ$，因其形状像心形又称心脏线．已知运动开始时点 $P$ 与点 $A(1,0)$ 重合．
以下说法正确的有 ( BCD )
  A．曲线 $Γ$ 上存在到原点的距离超过 $2\sqrt 3$ 的点
  B．点 $(1,2)$ 在曲线 $Γ$ 上
  C．曲线 $Γ$ 与直线 $x+y-2\sqrt2=0$ 有两个交点
  D．$\left|b\right|\leqslant \frac{3\sqrt3}2$

kuing

先求 `P` 的轨迹方程，如图：

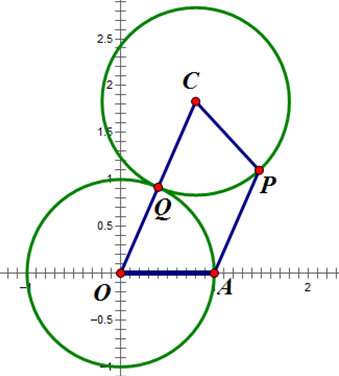
设两圆切点为 `Q`，由于无滑动，则 `\overparen{AQ} = \overparen{PQ}`，而两圆半径相同，所以 `\angle O=\angle C`，由此可见，四边形 `AOCP` 实际上是等腰梯形。

设 `Q(\cos\theta,\sin\theta)`，则易知 `AP=2(1-\cos\theta)`，由此即得 `P` 的轨迹的参数方程为
\[\led
x&=1+2(1-\cos\theta)\cos\theta,\\
y&=2(1-\cos\theta)\sin\theta.
\endled\]

对于选项 A，由 `\bigl(1+2(1-\cos\theta)\cos\theta\bigr)^2+\bigl(2(1-\cos\theta)\sin\theta\bigr)^2=5-4\cos\theta` 可知轨迹上的点到原点的最大距离为 `3`，小于 `2\sqrt3`，A 错；

对于选项 B，当 `\theta=\pi/2` 时点是 `(1,2)`，正确；

对于选项 C，由 B 正确知 `(1,2)` 在曲线上，而易知 `(1,2)` 在直线的上方，再看图可知曲线与此直线有两交点，正确；（其实这里不严格，严格起来很难写）

对于选项 D，由均值不等式有
\begin{align*}
b^2&=4(1-\cos\theta)^2\sin^2\theta\\
&=\frac43(1-\cos\theta)(1-\cos\theta)(1-\cos\theta)(3+3\cos\theta)\\
&\leqslant\frac43\left(\frac{1-\cos\theta+1-\cos\theta+1-\cos\theta+3+3\cos\theta}4\right)^4\\
&=\frac{27}4,
\end{align*}
开方即得 `\abs b\leqslant3\sqrt3/2`，正确。

isee

kuing 发表于 2025-3-22 17:05
先求 `P` 的轨迹方程，如图：

设两圆切点为 `Q`，由于无滑动，则 `\overparen{AQ} = \overparen{PQ}`，而 ...

由 C 坐标求 P，可能好理解些.

kuing

isee 发表于 2025-3-22 20:21
由 C 坐标求 P，可能好理解些.

一般情况通常是由 C 求 P，这题我见圆半径相等，有个等腰梯形，所以就换个写法。