关于$y$的三次方程的渐近解

hbghlyj

$x>0$时, 关于$y$的方程$$y^3+e^x y+x \log (x)=0$$有唯一实根$y_0$.
证明：存在常数$C$使$$-1<{y_0\over e^{-x} x \log (x)}\le C$$对任意$x>1$成立.
注：这里$e^{-x} x \log (x)$是AsymptoticSolve[y^3 + Exp[x] y + x Log[x] == 0, y, x->∞]算出的。

hbghlyj

$y_0=\frac{\sqrt[3]{\sqrt{3} \sqrt{27 x^2 \log ^2(x)+4 e^{3 x}}-9 x \log (x)}}{\sqrt[3]{2} 3^{2/3}}-\frac{\sqrt[3]{\frac{2}{3}} e^x}{\sqrt[3]{\sqrt{3} \sqrt{27 x^2 \log ^2(x)+4 e^{3 x}}-9 x \log (x)}}$

hbghlyj

如果在方程左边添加一项$e^{-x} x y^2 \log (x)$变成
$$y^3+e^x y+x \log (x)+e^{-x} x y^2 \log (x)=0$$
就可以因式分解
$$\left(y+i e^{x/2}\right) \left(y-i e^{x/2}\right) \left(y+e^{-x} x \log (x)\right)=0$$
得到$y=-e^{-x} x \log (x)$
当$x\to\infty$时$e^{-x} x y^2 \log (x)\to0$所以添加这一项应该不会改变很多？

hbghlyj

1. Plot[(-(((2/3)^(1/3) E^
2.     x)/(-9 x Log[x] + Sqrt[3] Sqrt[4 E^(3 x) + 27 x^2 Log[x]^2])^(
3.    1/3)) + (-9 x Log[x] + Sqrt[3] Sqrt[4 E^(3 x) + 27 x^2 Log[x]^2])^(
4.   1/3)/(2^(1/3) 3^(2/3)))/(E^-x x Log[x]), {x, 1, 10}]

复制代码

$\dfrac{y_0}{e^{-x} x \log (x)}$在$x\in(1,10)$的图象

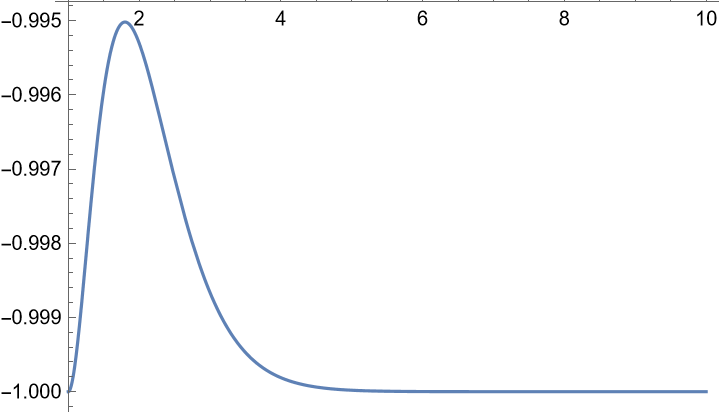
可见$-1< {y_0\over e^{-x} x \log (x)}\le C\approx-0.995$
而且当$x\to\infty$时趋于$-1$.
如何证明呢