与内心有关的一道小题

aishuxue

I为△ABC的内心,直线BI分别交AC及△ABC的外接圆于E,M 直线CI分别交AB及△ABC的外接圆于F,N, 求证:PA与△ABC的外接圆相切。

星奔川骛

pascal定理

乌贼

星奔川骛 发表于 2025-6-15 09:39
pascal定理

    原题等价于证明$ MN,EF,IG $三线共点。
如图：
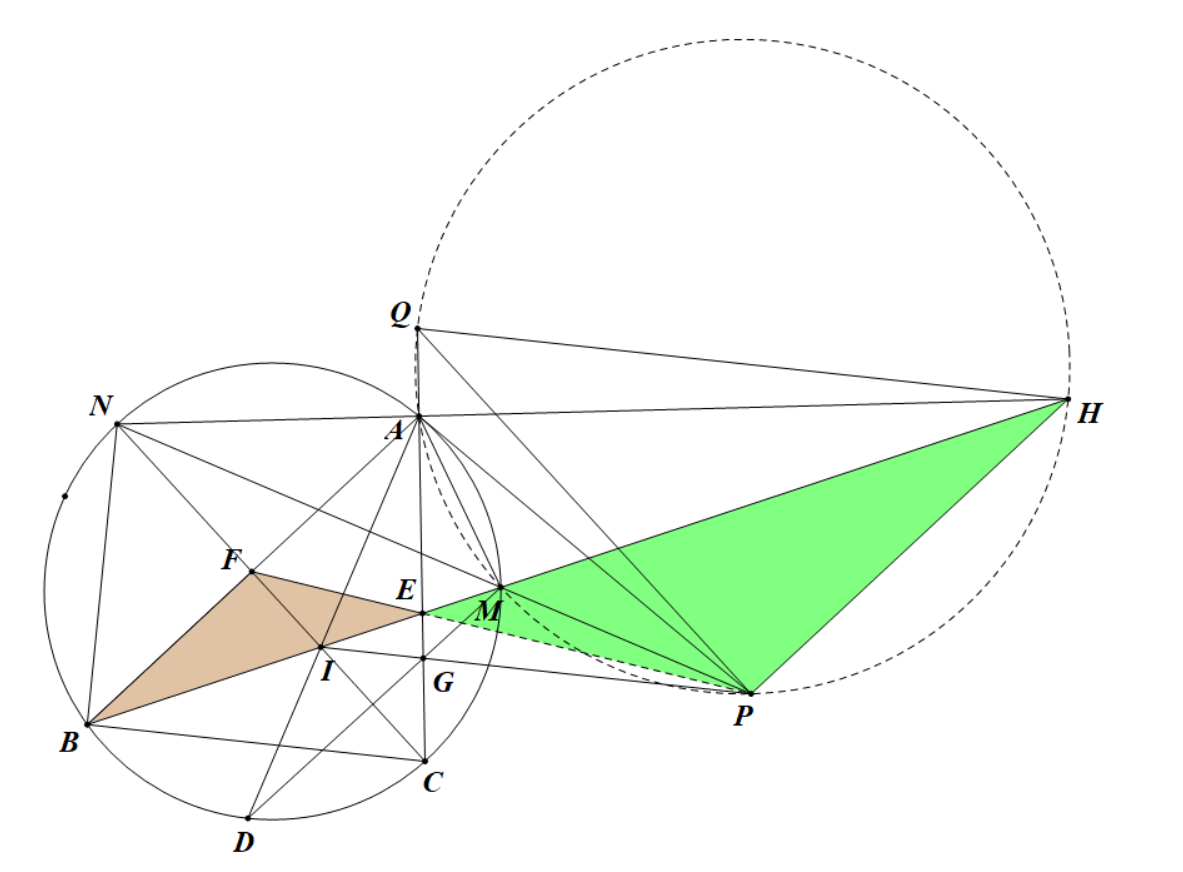
   $ P $为$ MN $与$ IG $交点，$ NP $垂直平分$ AI $,有\[ \angle PAM=\angle PIM \riff\angle PAC=\angle ABC \]  $ H $为$ NA $与$ BM $交点\[ \angle HMP=\angle BMN=\dfrac{1}{2}\angle ACB=\angle HAP \]即$ AHPM $四点共圆，有\[ \angle MHP=\angle MAP=\angle MBA\riff AB\px HP\riff\angle FBE=\angle PHE \]
作$ HQ\px BC $交$ CA $于$ Q $。有\[ \angle HQA=\angle ACB=\angle AMB \]有$ AQHM $四点共圆，即有$ AQHPM $五点共圆，又\[ \angle PQA=\angle AMN=\angle ACN\riff PQ\px CN \]故\[ \triangle FBC\sim \triangle PHQ\riff\dfrac{BF}{PH}=\dfrac{BC}{HQ}=\dfrac{BE}{HE}\riff\triangle FBE\sim \triangle PHE\riff\angle FEB=\angle HEP \]即有$ FEP $三点共线。

    但是不是只证明了原命题的逆命题？

乌贼

乌贼 发表于 2025-6-21 00:22
原题等价于证明$ MN,EF,IG $三线共点。
如图：
   $ P $为$ MN $与$ IG $交点，$ NP $垂直平分$ AI $, ...

只能作为引理使用，但如何直接证明呢？

1+1=？

是帕斯卡定理的五点退化

乌贼

乌贼 发表于 2025-6-21 12:59
只能作为引理使用，但如何直接证明呢？

直接证：
    $ PH\px AB $交$ BM $于$ H $，$ HQ\px BC $交$ CA $于$ Q $。有\[ \angle MHQ=\angle MBC=\angle MAC \]即$ AMHQ $四点共圆。
     又\[ \dfrac{BC}{HQ}=\dfrac{BE}{EH}=\dfrac{BF}{HP} \]\[ \angle FBC=\angle PHQ \]     所以\[ \triangle FBC\sim \triangle PHQ\riff \angle PQH=\angle BCF=\angle BMN=\angle PMH \]即有$ MPHQ $四点共圆。
     综上得$ AMPHQ $五点共圆，故\[ \angle MAP=\angle MHP=\angle MBA \]也就是$ AP $与$ \triangle ABC $的外接圆相切。